
设函数 (
( ),其中
),其中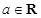 .
.
(Ⅰ)当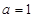 时,求曲线
时,求曲线 在点
在点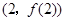 处的切线方程;
处的切线方程;
(Ⅱ)当 时,求函数
时,求函数 的极大值和极小值.
的极大值和极小值.
(Ⅰ)当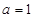 时,曲线
时,曲线 在点
在点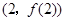 处的切线方程为
处的切线方程为 ;(Ⅱ)函数
;(Ⅱ)函数 在
在 处取得极小值
处取得极小值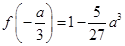 ,在
,在 处取得极大值
处取得极大值 .
.
【解析】
试题分析:(Ⅰ)把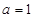 代入
代入 ,得
,得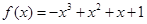 ,结合已知条件即可得切点的坐标为
,结合已知条件即可得切点的坐标为 .再对
.再对 求导,即可求得
求导,即可求得 ,即可得所求切线的斜率,最后利用直线方程的点斜式,即可得所求切线的方程;(Ⅱ)首先对
,即可得所求切线的斜率,最后利用直线方程的点斜式,即可得所求切线的方程;(Ⅱ)首先对 求导,得
求导,得 .令
.令 ,解得
,解得 或
或 .
.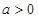 ,列出当
,列出当 变化时,
变化时, ,
, 随
随 的变化情况表格,即可求得当
的变化情况表格,即可求得当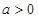 时,函数
时,函数 的极大值和极小值.
的极大值和极小值.
试题解析:(Ⅰ)当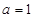 时,
时,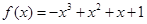 ,得
,得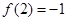 , 1分
, 1分
且 ,
, . 3分
. 3分
所以,曲线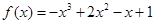 在点
在点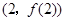 处的切线方程是
处的切线方程是 , 5分
, 5分
整理得 .
6分
.
6分
(Ⅱ)解: ,
, .
.
令 ,解得
,解得 或
或 .
8分
.
8分
若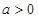 ,当
,当 变化时,
变化时, 的正负如下表:
的正负如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
因此,函数 在
在 处取得极小值
处取得极小值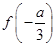 ,且
,且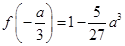 ;
;
函数 在
在 处取得极大值
处取得极大值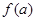 ,且
,且 .
12分
.
12分
考点:1.曲线切线方程的求法;2.利用导数求函数的极值.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
(05年天津卷理)(14分)
设函数![]()
(Ⅰ)证明![]() 其中为k为整数
其中为k为整数
(Ⅱ)设![]() 为
为![]() 的一个极值点,证明
的一个极值点,证明![]()
(Ⅲ)设![]() 在(0,+∞)内的全部极值点按从小到大的顺序排列为
在(0,+∞)内的全部极值点按从小到大的顺序排列为![]() ,证明:
,证明:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题16分) 设函数![]() ,且
,且![]() ,其中
,其中![]() 是自然对数的底数.(1)求
是自然对数的底数.(1)求![]() 与
与![]() 的关系;(2)若
的关系;(2)若![]() 在其定义域内为单调函数,求
在其定义域内为单调函数,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若在
,若在![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() >
>![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省五校协作体高三摸底考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分) 设函数f(x)=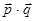 ,其中向量
,其中向量
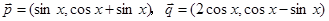 ,
,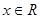 .
.
(1)求f( 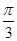 )的值及f( x)的最大值。
)的值及f( x)的最大值。
(2)求函数f( x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆市高三上学期第七次测试理科数学试卷(解析版) 题型:解答题
.设函数f(x)=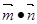 ,其中向量
,其中向量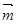 =(2cosx,1),
=(2cosx,1), 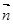 =(cosx,
=(cosx,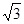 sin2x), x∈R.
sin2x), x∈R.
(1)
求f(x)的最小正周期;并求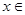
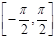 的值域和单调区间;
的值域和单调区间;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,f(A)=2,a=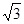 ,b+c=3(b>c),求b、c的长.
,b+c=3(b>c),求b、c的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com