
(本题满分14分)以下是有关椭圆的两个问题:
问题1:已知椭圆 ,定点A(1, 1),F是右焦点,P是椭圆上动点,则
,定点A(1, 1),F是右焦点,P是椭圆上动点,则 有最小值;
有最小值;
问题2:已知椭圆 ,定点A (2, 1),F是右焦点,
,定点A (2, 1),F是右焦点,
P是椭圆上动点, 有最小值;
有最小值;

(Ⅰ)求问题1中的最小值,并求此时P点坐标;
(Ⅱ)试类比问题1,猜想问题2中 的值,并谈谈你作此猜想的依据.
的值,并谈谈你作此猜想的依据.
.⑴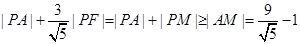 ,当且仅当A, P, M三点共线时取到最小值,此时点P的坐标为(
,当且仅当A, P, M三点共线时取到最小值,此时点P的坐标为(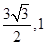 );
);
⑵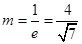 时|PA|+m|PF|=|PA|+med =|PA|+d,当P、A、B三点共线时,
时|PA|+m|PF|=|PA|+med =|PA|+d,当P、A、B三点共线时,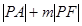 有最小值
有最小值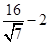 .
.
【解析】本试题主要是考查了椭圆中距离的最值问题的求解,
(1)在第一问题中利用第二定义可知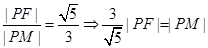
故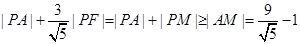 ,当且仅当A, P, M三点共线时取到最小值,此时点P的坐标为(
,当且仅当A, P, M三点共线时取到最小值,此时点P的坐标为(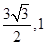 );
);
(2)猜想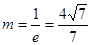 (8分)②理由:问题1中的数
(8分)②理由:问题1中的数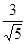 是椭圆的离心率的倒数,猜想问题2中的常数m也是椭圆离心率的倒数,也用上述的方法得到结论。
是椭圆的离心率的倒数,猜想问题2中的常数m也是椭圆离心率的倒数,也用上述的方法得到结论。
解:⑴注意到椭圆的离心率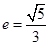 ,右焦点F(
,右焦点F(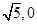 ),右准线
),右准线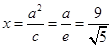 .过点P作准线的垂线,垂足为M,由椭圆第二定义,
.过点P作准线的垂线,垂足为M,由椭圆第二定义,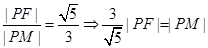
故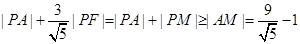 ,当且仅当A, P, M三点共线时取到最小值,此时点P的坐标为(
,当且仅当A, P, M三点共线时取到最小值,此时点P的坐标为(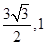 );(6分)
);(6分)
⑵①猜想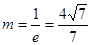 (8分)②理由:问题1中的数
(8分)②理由:问题1中的数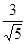 是椭圆的离心率的倒数,猜想问题2中的常数m也是椭圆离心率的倒数(9分)
是椭圆的离心率的倒数,猜想问题2中的常数m也是椭圆离心率的倒数(9分)
另一方面,从解题角度来看,问题1利用椭圆的第二定义,问题2也可利用类似方法解决最小值问题:设点P到椭圆的右准线距离为d,由椭圆第二定义,|PF|=ed,则|PA|+m|PF|=|PA|+med.当me=1,即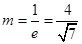 时|PA|+m|PF|=|PA|+med =|PA|+d,当P、A、B三点共线时,
时|PA|+m|PF|=|PA|+med =|PA|+d,当P、A、B三点共线时,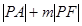 有最小值
有最小值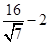 .(14分)(配合图像说明)
.(14分)(配合图像说明)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| π |
| 3 |
|
查看答案和解析>>
科目:高中数学 来源:2011-2012学年陕西省高三第一学期期中考试理科数学 题型:解答题
本题满分14分)
已知函数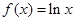 ,
,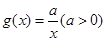 ,设
,设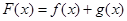 .
.
(Ⅰ)求函数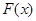 的单调区间;
的单调区间;
(Ⅱ)若以函数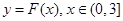 图像上任意一点
图像上任意一点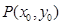 为切点的切线的斜率
为切点的切线的斜率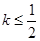 恒成立,求实数
恒成立,求实数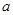 的最小值;
的最小值;
(Ⅲ)是否存在实数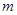 ,使得函数
,使得函数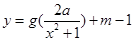 的图像与函数
的图像与函数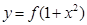 的图像恰有四个不同的交点?若存在,求出实数
的图像恰有四个不同的交点?若存在,求出实数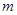 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省惠州市高三第三次调研考试数学理卷 题型:解答题
((本题满分14分)
已知梯形ABCD中,AD∥BC,∠ABC =∠BAD = ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
(1)当x=2时,求证:BD⊥EG ;
(2)若以F、B、C、D为顶点的三棱锥的体积记为 ,
,
求 的最大值;
的最大值;


(3)当 取得最大值时,求二面角D-BF-C的余弦值.
取得最大值时,求二面角D-BF-C的余弦值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省等三校高三2月月考数学理卷 题型:解答题
(本题满分14分)
已知椭圆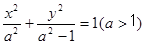 的左右焦点为
的左右焦点为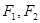 ,抛物线C:
,抛物线C: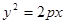 以F2为焦点且与椭圆相交于点M,直线F1M与抛物线C相切。
以F2为焦点且与椭圆相交于点M,直线F1M与抛物线C相切。
(Ⅰ)求抛物线C的方程和点M的坐标;
(Ⅱ)过F2作抛物线C的两条互相垂直的弦AB、DE,设弦AB、DE的中点分别为F、N,求证直线FN恒过定点;
查看答案和解析>>
科目:高中数学 来源:2010年广东省东莞市高二下学期期末考试(理科)数学卷 题型:解答题
(本题满分14分)已知以函数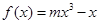 的图象上的点
的图象上的点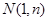 为切点的切线的倾斜角为
为切点的切线的倾斜角为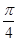 .
.
(1)求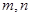 的值;
的值;
(2)是否存在正整数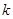 ,使不等式
,使不等式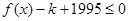 对于
对于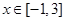 恒成立?若存在,求出最小的正整数
恒成立?若存在,求出最小的正整数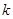 ,若不存在,说明理由;
,若不存在,说明理由;
(3)对于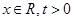 ,比较
,比较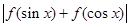 与
与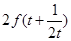 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com