
分析 (1)直接借助于直线系方程可得方程组$\left\{\begin{array}{l}{x+2=0}\\{1-y=0}\end{array}\right.$,求解方程组可得直线l恒过一个定点的坐标;
(2)把当-3<x<3时,直线上的点都在x轴上方,转化为$\left\{\begin{array}{l}{f(-3)=-3k+2k+1≥0}\\{f(3)=3k+2k+1≥0}\end{array}\right.$,求解不等式组得答案.
解答 (1)证明:由y=kx+2k+1,得k(x+2)+1-y=0,
联立$\left\{\begin{array}{l}{x+2=0}\\{1-y=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$,
∴直线l:y=kx+2k+1过定点(-2,1);
(2)解:令f(x)=kx+2k+1,
∵当-3<x<3时,直线上的点都在x轴上方,
∴$\left\{\begin{array}{l}{f(-3)=-3k+2k+1≥0}\\{f(3)=3k+2k+1≥0}\end{array}\right.$,解得-$\frac{1}{5}≤k≤1$.
∴实数k的取值范围是$[-\frac{1}{5},1]$.
点评 本题考查直线系方程,考查了一次函数的性质,体现了数学转化思想方法,是基础题.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,-e-$\frac{4}{e+1}$) | B. | (-4,-3) | C. | (-e-$\frac{4}{e+1}$,-3) | D. | (-e-$\frac{4}{e+1}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$,$\frac{3π}{4}$ | B. | $\frac{3π}{4}$,$\frac{5π}{4}$ | C. | $\frac{5π}{4}$ | D. | $\frac{5π}{4}$,$\frac{7π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≥8或m≤-2 | B. | m≥8 | C. | m≤-2 | D. | -2≤x≤8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
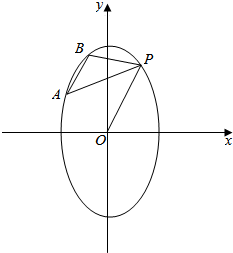 点P在椭圆3x2+y2=12上,OP倾斜角为60°,AB∥OP,A,B在椭圆上且都在x轴上方,求△ABP面积的最大值及此时直线AB的方程.
点P在椭圆3x2+y2=12上,OP倾斜角为60°,AB∥OP,A,B在椭圆上且都在x轴上方,求△ABP面积的最大值及此时直线AB的方程.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com