
【题目】已知二次函数![]() 的图象的顶点坐标为
的图象的顶点坐标为![]() ,且过坐标原点
,且过坐标原点![]() .数列
.数列![]() 的前
的前![]() 项和为
项和为![]() ,点
,点![]() 在二次函数
在二次函数![]() 的图象上.
的图象上.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)在数列![]() 中是否存在这样一些项:
中是否存在这样一些项:![]()
![]()
![]() ,这些项都能够构成以
,这些项都能够构成以![]() 为首项,
为首项,![]() 为公比的等比数列
为公比的等比数列![]() ?若存在,写出
?若存在,写出![]() 关于
关于![]() 的表达式;若不存在,说明理由.
的表达式;若不存在,说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() (Ⅲ)存在,
(Ⅲ)存在,![]()
【解析】
试题(Ⅰ)由已知可得数列![]() 的前
的前![]() 项和为
项和为![]() 的公式,再利用
的公式,再利用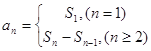 求得数列
求得数列![]() 的通项公式;
的通项公式;
(Ⅱ)分n为奇数与偶数先求出![]() ,由使
,由使![]() 对
对![]() 恒成立,通过分离参数t转化为求函数的最值,即可求得实数
恒成立,通过分离参数t转化为求函数的最值,即可求得实数![]() 的取值范围;
的取值范围;
(Ⅲ)由![]() 知,数列
知,数列![]() 中每一项都不可能是偶数,假设存在,对q的每一个取值:1,2,3,4逐一讨论即可获得结论.
中每一项都不可能是偶数,假设存在,对q的每一个取值:1,2,3,4逐一讨论即可获得结论.
试题解析:(Ⅰ)由题意可知![]()
所以![]()
当![]() 时,
时,![]()
当![]() 时
时![]() 适合上式
适合上式
所以,数列![]() 的通项公式为
的通项公式为![]()
(Ⅱ)因为![]()
所以![]()
![]()
由(Ⅰ)可知,数列![]() 是以1为首项,公差为
是以1为首项,公差为![]() 的等差数列.
的等差数列.
当![]() 时,
时,
![]()
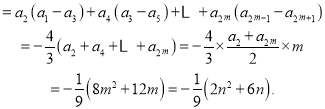
当![]() 时,
时,
![]()
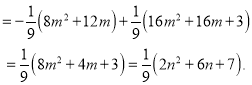
所以 ;
;
要使![]() 对
对![]() 恒成立,
恒成立,
只要使![]() 为正偶数)恒成立.
为正偶数)恒成立.
即使![]() 对
对![]() 为正偶数恒成立,
为正偶数恒成立,
故实数![]() 的取值范围是
的取值范围是![]()
(Ⅲ)由![]() 知,数列
知,数列![]() 中每一项都不可能是偶数.
中每一项都不可能是偶数.
如存在以![]() 为首项,公比
为首项,公比![]() 为2或4的数列
为2或4的数列![]() ,此时
,此时![]() 中每一项除第一项外都是偶数,故不存在以
中每一项除第一项外都是偶数,故不存在以![]() 为首项,公比为偶数的数列
为首项,公比为偶数的数列![]() .
.
当![]() 时,显然不存在这样的数列
时,显然不存在这样的数列![]() .
.
当![]() 时,若存在以
时,若存在以![]() 为首项,公比为3的数列
为首项,公比为3的数列![]() ,则
,则![]()
![]()
所以存在满足条件的数列![]() ,且
,且![]()


科目:高中数学 来源: 题型:
【题目】下列有关命题的说法中错误的是( )
A. 若![]() 为真命题,则
为真命题,则![]() 中至少有一个为真命题.
中至少有一个为真命题.
B. 命题:“若![]() 是幂函数,则
是幂函数,则![]() 的图象不经过第四象限”的否命题是假命题.
的图象不经过第四象限”的否命题是假命题.
C. 命题“![]() ,有
,有![]() 且
且![]() ”的否定形式是“
”的否定形式是“![]() ,有
,有![]() 且
且![]() ”.
”.
D. 若直线![]() 和平面
和平面![]() ,满足
,满足![]() .则“
.则“![]() ” 是“
” 是“![]() ”的充分不必要条件.
”的充分不必要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】总体由编号为01,02,…,49,50的50个个体组成,利用下面的随机数表选取6个个体,选取方法是从随机数表第7行的第9列和第10列数字开始从左到右依次选取两个数字,则选出的第4个个体的编号为( )
附:第6行至第8行的随机数表
2748 6198 7164 4148 7086 2888 8519 1620 7477
0111 1630 2404 2979 7991 9624 5125 3211 4919
7306 4916 7677 8733 9974 6732 2635 7900 3370
A.11B.24C.25D.20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设y=f(x)在(-∞,1]上有定义,对于给定的实数K,定义fK(x)=![]() ,给出函数f(x)=2x+1-4x,若对于任意x∈(-∞,1],恒有fK(x)=f(x),则( )
,给出函数f(x)=2x+1-4x,若对于任意x∈(-∞,1],恒有fK(x)=f(x),则( )
A.K的最大值为0
B.K的最小值为0
C.K的最大值为1
D.K的最小值为1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,x∈[-1,1],函数
,x∈[-1,1],函数![]() ,a∈R的最小值为h(a).
,a∈R的最小值为h(a).
(1)求h(a)的解析式;
(2)是否存在实数m,n同时满足下列两个条件:①m>n>3;②当h(a)的定义域为[n,m]时,值域为[n2,m2]?若存在,求出m,n的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项的和为
项的和为![]() 且
且![]() 数列
数列![]() 满足
满足![]() 且对任意正整数
且对任意正整数![]() 都有
都有![]() 成等比数列.
成等比数列.
(1)求数列![]() 的通项公式.
的通项公式.
(2)证明数列![]() 为等差数列.
为等差数列.
(3)令![]() 问是否存在正整数
问是否存在正整数![]() 使得
使得![]() 成等比数列?若存在,求出
成等比数列?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|+3x,其中a>0.
(1)当a=1时,求不等式f(x)>3x+2的解集;
(2)若不等式f(x)≤0的解集为{x|x≤﹣1},求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了测量某塔的高度,某人在一条水平公路![]() 两点进行测量.在
两点进行测量.在![]() 点测得塔底
点测得塔底![]() 在南偏西
在南偏西![]() ,塔顶仰角为
,塔顶仰角为![]() ,此人沿着南偏东
,此人沿着南偏东![]() 方向前进10米到
方向前进10米到![]() 点,测得塔顶的仰角为
点,测得塔顶的仰角为![]() ,则塔的高度为( )
,则塔的高度为( )
A. 5米B. 10米C. 15米D. 20米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com