
已知函数f(x)=ax+x2-xlna(a>0,a≠1).
(1)当a>1时,求证:函数f(x)在(0,+∞)上单调递增;
(2)若函数y=|f(x)-t|-1有三个零点,求t的值;
(3)若存在x1,x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1,试求a的取值范围.
(1)见解析;(2)t=2;(3)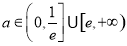
【解析】试题分析:(1)通过f '(x)≥0(a>0)恒成立可证;(2)要使得函数y=|f(x)-t|-1有三个零点,只需其极大值大于0,而极小值小于0即可;(3)要满足题意,只需在x∈[-1,1]时函数的最大值与最小值之差不小于e-1即可.
解析:(1)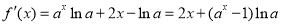
由于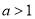 ,故当
,故当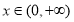 时,
时,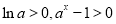 ,所以
,所以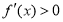 ,
,
故函数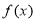 在
在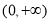 上单调递增. 4分
上单调递增. 4分
(2)当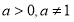 时,因为
时,因为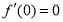 ,且
,且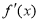 在R上单调递增,
在R上单调递增,
故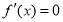 有唯一解
有唯一解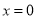 .
.
所以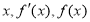 的变化情况如下表所示:
的变化情况如下表所示:
x |
| 0 |
|
| - | 0 | + |
| 递减 | 极小值 | 递增 |
又函数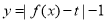 有三个零点,所以方程
有三个零点,所以方程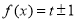 有三个根,
有三个根,
而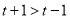 ,所以
,所以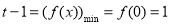 ,解得
,解得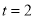 . 10分
. 10分
(3)因为存在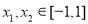 ,使得
,使得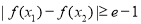 ,
,
所以当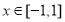 时,
时,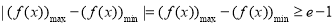 .
.
由(2)知,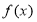 在
在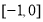 上递减,在
上递减,在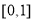 上递增,
上递增,
所以当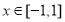 时,
时,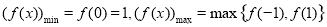 .
.
而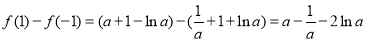 ,
,
记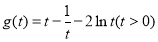 ,因为
,因为 (当
(当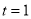 时取等号),
时取等号),
所以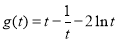 在
在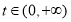 上单调递增.
上单调递增.
而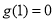 ,故当
,故当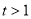 时,
时,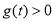 ;当
;当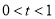 时,
时,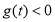 .即当
.即当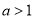 时,
时,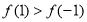 ;
;
当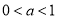 时,
时,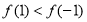 .
.
①当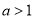 时,由
时,由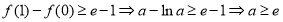 ;
;
②当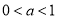 时,由
时,由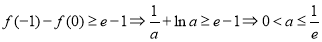 .
.
综上可知,所求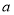 的取值范围为
的取值范围为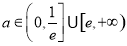 . 14分
. 14分
考点:利用导数研究函数性质,函数的单调性,零点,极值,不等式


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源:2013-2014学年山东省高三12月月考文科数学试卷(解析版) 题型:解答题
已知函数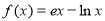 ,
,
(1)求函数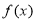 的单调区间;
的单调区间;
(2)在区间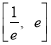 内存在
内存在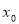 ,使不等式
,使不等式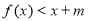 成立,求
成立,求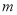 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省菏泽市高三3月模拟考试理科数学试卷(解析版) 题型:选择题
已知复数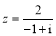 ,则( )
,则( )
A.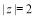 B.z的实部为1 C.z的虚部为﹣1 D.z的共轭复数为1+i
B.z的实部为1 C.z的虚部为﹣1 D.z的共轭复数为1+i
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省烟台市高三统一质量检测考试理科数学试卷(解析版) 题型:解答题
已知椭圆C的中点在原点,焦点在x轴上,离心率等于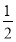 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线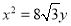 的焦点.
的焦点.
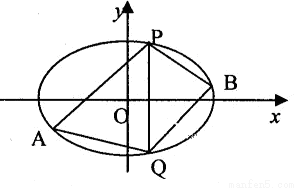
(1)求椭圆C的方程;
(2)己知点P(2,3),Q(2,-3)在椭圆上,点A、B是椭圆上不同的两个动点,且满足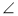 APQ=
APQ=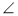 BPQ,试问直线AB的斜率是否为定值,请说明理由.
BPQ,试问直线AB的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都实验外国语高三11月月考文科数学试卷(解析版) 题型:解答题
已知函数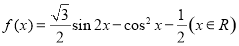
(1)当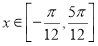 时,求函数
时,求函数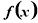 取得最大值和最小值时
取得最大值和最小值时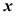 的值;
的值;
(2)设锐角△ABC的内角A、B、C的对应边分别是a,b,c,且a=1,c∈N*,若向量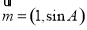 与向量
与向量 平行,求c的值.
平行,求c的值.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都实验外国语高三11月月考文科数学试卷(解析版) 题型:选择题
设函数 ,其中[x]表示不超过x的最大整数,如[-1.3]=-2,[1.3]=1,则函数y=f(x)-
,其中[x]表示不超过x的最大整数,如[-1.3]=-2,[1.3]=1,则函数y=f(x)-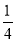 x-
x-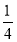 不同零点的个数为( )
不同零点的个数为( )
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省烟台市高三统一质量检测考试理科数学试卷(解析版) 题型:选择题
已知不重合的直线m、l和平面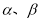 ,且
,且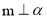 ,
,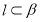 .给出下列命题:
.给出下列命题:
①若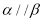 ,则
,则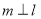 ;
;
②若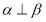 ,则
,则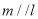 ;
;
③若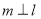 ,则
,则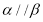 ;
;
④若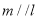 ,则
,则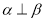 ,
,
其中正确命题的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com