
【题目】如图,在四棱锥![]() 中,
中,![]() 为平行四边形,
为平行四边形,![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
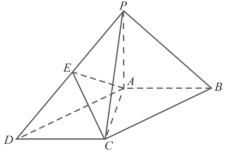
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上(不含端点)是否存在一点
上(不含端点)是否存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,确定
?若存在,确定![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【答案】(1)见解析(2)存在,![]()
【解析】
(1)连接![]() 交
交![]() 于
于![]() 点,由三角形中位线性质知
点,由三角形中位线性质知![]() ,由线面平行判定定理证得结论;
,由线面平行判定定理证得结论;
(2)以![]() 为原点建立空间直角坐标系,假设
为原点建立空间直角坐标系,假设![]() ,可用
,可用![]() 表示出
表示出![]() 点坐标;根据二面角的向量求法可根据二面角的余弦值构造出关于
点坐标;根据二面角的向量求法可根据二面角的余弦值构造出关于![]() 的方程,从而解得结果.
的方程,从而解得结果.
(1)连接![]() 交
交![]() 于
于![]() 点,连接
点,连接![]() ,
,

![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]() 为
为![]() 中点,又
中点,又![]() 为
为![]() 中点,
中点,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)![]() 平面
平面![]() ,
,![]() ,
,![]() 两两互相垂直,
两两互相垂直,
则以![]() 为坐标原点,可建立如下图所示的空间直角坐标系:
为坐标原点,可建立如下图所示的空间直角坐标系:

则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() ,且
,且![]() ,
,
则![]() ,
,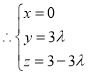 ,即
,即![]() ,
,
设平面![]() 的法向量
的法向量![]() ,又
,又![]() ,
,![]() ,
,
则 ,令
,令![]() ,则
,则![]() ,
,![]() ,
,![]() ;
;
设平面![]() 的一个法向量
的一个法向量![]() ,又
,又![]() ,
,![]() ,
,
则 ,令
,令![]() ,则
,则![]() ,
,![]() ,
,![]() ;
;
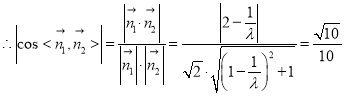 ,解得:
,解得:![]() 或
或![]() ,
,
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() ,
,![]() 二面角
二面角![]() 为锐二面角,
为锐二面角,
![]() 不满足题意,舍去,即
不满足题意,舍去,即![]() .
.
![]() 在线段
在线段![]() 上存在点
上存在点![]() ,
,![]() 时,二面角
时,二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】2019年末,武汉出现新型冠状病毒(![]() 肺炎疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,目前没有特异治疗方法.防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,某社区将本社区的排查工作人员分为
肺炎疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,目前没有特异治疗方法.防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,某社区将本社区的排查工作人员分为![]() ,
,![]() 两个小组,排查工作期间社区随机抽取了100户已排查户,进行了对排查工作态度是否满意的电话调查,根据调查结果统计后,得到如下
两个小组,排查工作期间社区随机抽取了100户已排查户,进行了对排查工作态度是否满意的电话调查,根据调查结果统计后,得到如下![]() 的列联表.
的列联表.
是否满意 组别 | 不满意 | 满意 | 合计 |
| 16 | 34 | 50 |
| 2 | 45 | 50 |
合计 | 21 | 79 | 100 |
(1)分别估计社区居民对![]() 组、
组、![]() 组两个排查组的工作态度满意的概率;
组两个排查组的工作态度满意的概率;
(2)根据列联表的数据,能否有![]() 的把握认为“对社区排查工作态度满意”与“排查工作组别”有关?
的把握认为“对社区排查工作态度满意”与“排查工作组别”有关?
附表:
|
|
|
|
|
|
|
|
|
|
|
|
附: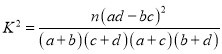
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图①是一栋新农村别墅,它由上部屋顶和下部主体两部分组成.如图②,屋顶由四坡屋面构成,其中前后两坡屋面ABFE和CDEF是全等的等腰梯形,左右两坡屋面EAD和FBC是全等的三角形.点F在平面ABCD和BC上的射影分别为H,M.已知HM 5 m,BC 10 m,梯形ABFE的面积是△FBC面积的2.2倍.设∠FMH ![]()
![]() .
.
(1)求屋顶面积S关于![]() 的函数关系式;
的函数关系式;
(2)已知上部屋顶造价与屋顶面积成正比,比例系数为k(k为正的常数),下部主体造价与其 高度成正比,比例系数为16 k.现欲造一栋上、下总高度为6 m的别墅,试问:当![]() 为何值时,总造价最低?
为何值时,总造价最低?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂制作如图所示的一种标识,在半径为R的圆内做一个关于圆心对称的“H型”图形,“H”型图形由两竖一横三个等宽的矩形组成,两个竖直的矩形全等且它们的长边是横向矩形长边的![]() 倍,设O为圆心,
倍,设O为圆心,![]() ,“H”型图形的面积为S.
,“H”型图形的面积为S.
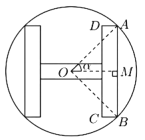
(1)将AB、AD用R、![]() 表示,并将S表示成
表示,并将S表示成![]() 的函数;
的函数;
(2)为了突出“H”型图形,设计时应使S尽可能大,则当![]() 为何值时,S最大?并求出S的最大值.
为何值时,S最大?并求出S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点P为平面上的动点,过点P作直线l:
,点P为平面上的动点,过点P作直线l:![]() 的垂线,垂足为Q,且
的垂线,垂足为Q,且![]() .
.
![]() Ⅰ
Ⅰ![]() 求动点P的轨迹C的方程;
求动点P的轨迹C的方程;
![]() Ⅱ
Ⅱ![]() 设点P的轨迹C与x轴交于点M,点A,B是轨迹C上异于点M的不同的两点,且满足
设点P的轨迹C与x轴交于点M,点A,B是轨迹C上异于点M的不同的两点,且满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村共有100户农民,且都从事蔬菜种植,平均每户的年收入为2万元.为了调整产业结构,该镇政府决定动员部分农民从事蔬菜加工.据估计,若能动员![]() 户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入比上一年提高
户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入比上一年提高![]() ,而从事蔬菜加工的农民平均每户的年收入为
,而从事蔬菜加工的农民平均每户的年收入为![]() 万元.
万元.
(1)在动员![]() 户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前100户农民的总年收入,求
户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前100户农民的总年收入,求![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,要使这100户农民中从事蔬菜加工的农民的总年收入始终不高于从事蔬菜种植的农民的总年收入,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com