
(Ⅰ)求椭圆的方程及离心率;
(Ⅱ)若![]() ·
·![]() =0,求直线PQ的方程;
=0,求直线PQ的方程;
22. 本小题主要考查椭圆的标准方程和几何性质,直线方程、平面向量的计算,曲线和方程的关系等解析几何的基本思想方法和综合解题能力.
(Ⅰ)解:由题意,可设椭圆的方程为![]() +
+![]() =1(a>
=1(a>![]() ).
).
由已知得
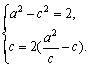
解得a=![]() ,c=2.
,c=2.
所以椭圆的方程为![]() +
+![]() =1,离心率e=
=1,离心率e=![]() .
.
(Ⅱ)解:由(Ⅰ)可得A(3,0).
设直线PQ的方程为y=k(x-3),由方程组
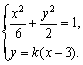
得(3k2+1)x2-18k2x+27k2-6=0.
依题意Δ=12(2-3k2)>0,得-![]() <k<
<k<![]() .
.
设P(x1,y1),Q(x2,y2),则
x1+x2=![]() , ①
, ①
x1x2=![]() . ②
. ②
由直线PQ的方程得y1=k(x1-3),y2=k(x2-3).于是
y1y2=k2(x1-3)(x2-3)=k2[x1x2-3(x1+x2)+9]. ③
∵![]() ·
·![]() =0, ∴x1x2+y1y2=0. ④
=0, ∴x1x2+y1y2=0. ④
由①②③④得5k2=1,从而k=±![]() ∈(-
∈(-![]() ,
,![]() ).
).
所以直线PQ的方程为x-![]() y-3=0或x+
y-3=0或x+![]() y-3=0.
y-3=0.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
| 2 |
| OP |
| OQ |
| AP |
| AQ |
| FM |
| FQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| OP |
| OQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| AO |
| AQ |
| AP |
| FQ′ |
| FP |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 |
查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学选修1-1 2.2椭圆练习卷(解析版) 题型:解答题
椭圆的中心是原点O,它的短轴长为 ,相应于焦点F(c,0)(
,相应于焦点F(c,0)( )的准线
)的准线 与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点 .
与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点 .
(1)求椭圆的方程及离心率;
(2)若 ,求直线PQ的方程;
,求直线PQ的方程;
(3)设 (
( ),过点P且平行于准线
),过点P且平行于准线 的直线与椭圆相交于另一点M,证明
的直线与椭圆相交于另一点M,证明 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com