
| 运行次数n | 输出y的值 为1的频数 | 输出y的值 为2的频数 | 输出y的值 为3的频数 |
| 30 | 14 | 6 | 10 |
| … | … | … | … |
| 2 100 | 1 027 | 376 | 697 |
| 运行次数n | 输出y的值 为1的频数 | 输出y的值 为2的频数 | 输出y的值 为3的频数 |
| 30 | 12 | 11 | 7 |
| … | … | … | … |
| 2 100 | 1 051 | 696 | 353 |

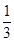

| ξ | 0 | 1 | 2 | 3 |
| P |  |  |  |  |
 +1×
+1× +2×
+2× +3×
+3× =1
=1 ;
;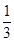 ;
; .
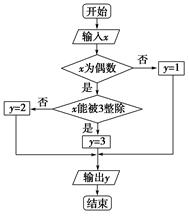
. ,输出y的值为2的概率为
,输出y的值为2的概率为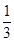 ,输出y的值为3的概率为
,输出y的值为3的概率为 .
.| | 输出y的值 为1的频率 | 输出y的值 为2的频率 | 输出y的值 为3的频率 |
| 甲 | 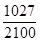 | 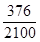 |  |
| 乙 | 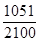 |  | 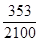 |
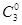 ×
×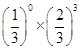 =
= ,
, ×
× =
= ,
, ×
×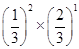 =
= ,
,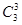 ×
× =
= .
.| ξ | 0 | 1 | 2 | 3 |
| P |  |  |  |  |
 +1×
+1× +2×
+2× +3×
+3× =1.
=1.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
| PM2.5日均值m(微克/立方米) | 空气质量等级 |
 | 一级 |
 | 二级 |
 | 超标 |

 表示空气质量达到一级的天数,求
表示空气质量达到一级的天数,求 的分布列;
的分布列;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 分的次数为
分的次数为 ,求
,求 的分布列和数学期望
的分布列和数学期望 ..
..查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,B级考试合格的概率为
,B级考试合格的概率为 .假设各级考试成绩合格与否均互不影响.
.假设各级考试成绩合格与否均互不影响. ,求
,求 的数学期望E
的数学期望E .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com