
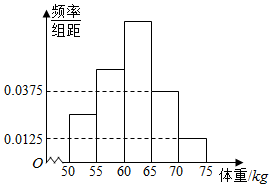
 ij��УΪ�˽⼴����ҵ���д�ѧ��������״���������960���д�ѧ�������أ���λ��kg�����������ݶ�������[50��75]�У���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��ͼ�д����ҵ�ǰ3��С���Ƶ��֮��Ϊ1��2��3��
ij��УΪ�˽⼴����ҵ���д�ѧ��������״���������960���д�ѧ�������أ���λ��kg�����������ݶ�������[50��75]�У���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��ͼ�д����ҵ�ǰ3��С���Ƶ��֮��Ϊ1��2��3������ ��1������С���ε����=Ƶ�ʣ������������ǰ�����Ƶ�ʣ�����Ƶ��=Ƶ�ʡ������������õ�����С��60kg�ĸ�������������
��2���ֱ����60��65�г��4����65��70�г��2�������������6���д�ѧ�������ѡȡ2���ķ����Լ�������һ���д�ѧ�����ش���65kg�ķ������Ӷ�������������ĸ��ʼ��ɣ�
��� �⣺��1������ֱ��ͼ�и������ε����֮��Ϊ1����4�͵�5���Ƶ�ʺ�Ϊ��0.0375+0.0125����5=0.25��
��֪ǰ3��С���Ƶ��֮��Ϊ1-0.25=0.75��
�ߴ����ҵ�ǰ3��С���Ƶ��֮��Ϊ1��2��3��
����ǰ2���Ƶ��Ϊ0.75��$\frac{3}{6}$=0.375��
������С��60kg�ĸ�����������Ϊ960��0.375=360��
��2��60��65��ѧ������0.375��960=360�ˣ�
65��70��ѧ������0.0375��5��960=180�ˣ�
��������60��70kg��Χ���д�ѧ�����÷ֲ�����ķ���ѡȡ6����
��60��65��4����65��70��2����
�ٴ���6���д�ѧ�������ѡȡ2������${C}_{6}^{2}$=15�ַ�����
������һ���д�ѧ�����ش���65kg��${{C}_{4}^{1}C}_{2}^{1}$+${C}_{2}^{2}$=9�֣�
��P��A��=$\frac{9}{15}$=$\frac{3}{5}$��
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ�����֪ʶ������ֲ�����Լ��ŵ�������⣬ֱ��ͼ�еĸ������ε����������Ƶ�ʣ����Ը����������֮��Ϊ1����������=$\frac{Ƶ��}{Ƶ��}$�����ڻ����⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֱ��l��ƽ���ƽ�У���l��ƽ����ڵ�����һ��ֱ�߶�û�й����� | |
| B�� | ��ֱ��l��ƽ���ƽ�У���l��ƽ����ڵ�����һ��ֱ�߶�ƽ�� | |
| C�� | ��ֱ��l�����������㲻��ƽ����ڣ���l�Φ� | |
| D�� | �������ƽ�����е�һ����һ��ƽ��ƽ�У���ô��һ��Ҳ�����ƽ��ƽ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{2}$ | B�� | $\frac{\sqrt{5}-1}{2}$ | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����ͦ£����ɦ�=m��n��m����n�ͦ���n�ͦ� | B�� | �����Φ£�m?����n?������m��n | ||
| C�� | ��m�ͦ���n�ͦ£����Φ£���m��n | D�� | �����ɦ�=m��n��m����n�Φ�����n�Φ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com