
| A. | 若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点 | |
| B. | 若直线l与平面α平行,则l与平面α内的任意一条直线都平行 | |
| C. | 若直线l上有无数个点不在平面α内,则l∥α | |
| D. | 如果两条平行线中的一条与一个平面平行,那么另一条也与这个平面平行 |
分析 A用反证法易知命题正确;
B直线l与平面α内的任意一条直线无公共点时,两直线的位置关系是平行或异面;
C直线与平面相交时,有无数个点不在平面内;
D两条平行线中的一条与一个平面平行,另一条与这个平面平行或在平面内.
解答 解:对于A,用反证法易知,直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点,命题正确;
对于B,若直线l与平面α平行,则l与平面α内的任意一条直线无公共点,
所以l与平面α内的任一条直线有两种位置关系:平行或异面,B错误;
对于C,若直线与平面相交,则除了交点以外的无数个点都不在平面内,所以命题错误;
对于D,如果两条平行线中的一条与一个平面平行,那么另一条与这个平面平行或在平面内,所以命题错误.
故选:A.
点评 本题主要考查了空间中直线与平面之间的位置关系与应用问题,也考查了空间想象能力和思维能力,是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
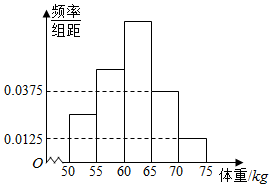 某高校为了解即将毕业的男大学生的身体状况,检测了960名男大学生的体重(单位:kg),所得数据都在区间[50,75]中,其频率分布直方图如图所示,图中从左到右的前3个小组的频率之比为1:2:3.
某高校为了解即将毕业的男大学生的身体状况,检测了960名男大学生的体重(单位:kg),所得数据都在区间[50,75]中,其频率分布直方图如图所示,图中从左到右的前3个小组的频率之比为1:2:3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com