
���� �ڡ�ABC�и������Ҷ������sin��ACB=$\frac{sin30��}{AC}$•AB=$\frac{\sqrt{3}}{2}$���ɵá�ACB=120�㣬�Ӷ��õ�BC=AC=1�������õ���ACD�DZ߳�Ϊ1�ȱ������Σ���CD=1ǧ�ף����ɼ��Ա����ʻ�ٶȺ�BC��CD�����������������Ҫ��ʱ�䣮
��� 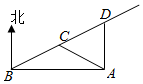 �⣺��ͼ��ʾ������ΪA����鿪ʼ��ΪB��
�⣺��ͼ��ʾ������ΪA����鿪ʼ��ΪB��
�蹫·��C��D���㵽����ľ���Ϊ1ǧ�ף�
�ڡ�ABC�У�AB=$\sqrt{3}$��ǧ�ף���AC=1��ǧ�ף�����ABC=30�㣬
�����Ҷ���sin��ACB=$\frac{sin30��}{AC}$•AB=$\frac{\sqrt{3}}{2}$��
���ACB=120�㣨��ACB=60�㲻�����⣩�����BAC=30�㣬��BC=AC=1��ǧ�ף���
�ڡ�ACD�У�AC=AD����ACD=60�㣬���ACDΪ�ȱ������Σ���CD=1��ǧ�ף���
��$\frac{BC}{12}$��60=5������BC����5���ӣ�CD����5���ӣ�
�������Ҫ5���Ӽ��Ա��ʼ�ղ����źţ�����������5���Ӳ���ϸ�
���� �������ʵ��Ӧ�����⣬����Ա����ź���Ҫ��ʱ�䣮���ؿ��������Ҷ����ͽ������ε�ʵ��Ӧ�õ�֪ʶ�������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �տ� | ���տ� | �ϼ� | |
| 45������ | |||
| 45�꼰���� | |||
| �ϼ� |
| P��K2��k0�� | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֱ��l��ƽ���ƽ�У���l��ƽ����ڵ�����һ��ֱ�߶�û�й����� | |
| B�� | ��ֱ��l��ƽ���ƽ�У���l��ƽ����ڵ�����һ��ֱ�߶�ƽ�� | |
| C�� | ��ֱ��l�����������㲻��ƽ����ڣ���l�Φ� | |
| D�� | �������ƽ�����е�һ����һ��ƽ��ƽ�У���ô��һ��Ҳ�����ƽ��ƽ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1��m��$\frac{2}{3}$ | B�� | m��$\frac{2}{3}$ | C�� | m��$\frac{2}{3}$��m��-1 | D�� | m��$\frac{2}{3}$��m��-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\frac{3}{2}$ | C�� | $\frac{5}{2}$ | D�� | 3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com