
已知圆心在第二象限内,半径为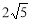 的圆
的圆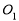 与
与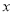 轴交于
轴交于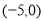 和
和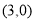 两点.
两点.
(1)求圆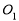 的方程;
的方程;
(2)求圆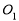 的过点A(1,6)的切线方程;
的过点A(1,6)的切线方程;
(3)已知点N(9,2)在(2)中的切线上,过点A作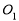 N的垂线,垂足为M,点H为线段AM上异于两个端点的动点,以点H为中点的弦与圆交于点B,C,过B,C两点分别作圆的切线,两切线交于点P,求直线
N的垂线,垂足为M,点H为线段AM上异于两个端点的动点,以点H为中点的弦与圆交于点B,C,过B,C两点分别作圆的切线,两切线交于点P,求直线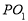 的斜率与直线PN的斜率之积.
的斜率与直线PN的斜率之积.

(1) ;(2)
;(2) ;(3)-1 .
;(3)-1 .
【解析】
试题分析:(1)根据圆的圆心坐标和半径求圆的标准方程.(2)直线和圆相交,根据半径,弦长的一半,圆心距求弦长.(3)圆的弦长的常用求法:几何法求圆的半径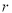 ,弦心距
,弦心距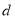 ,弦长
,弦长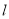 ,则
,则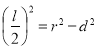 ;
;
(4)在求切线方程时,应先选择适当的直线方程的形式,并注意各种形式的适用条件,用斜截式和点斜式时,直线的斜率必须存在,而两点式不能表示与坐标轴垂直的直线,截距式不能表示与坐标轴垂直或过原点的直线;
试题解析:(1)由题知圆与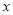 轴交于
轴交于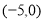 和
和 ,所以,圆心可设为
,所以,圆心可设为 ,又半径为
,又半径为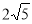 ,则
,则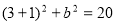 ,得
,得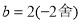 ,
,
所以,圆的方程为 .
.
(2)由题知,点A(1,6)在圆上,所以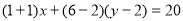 ,
,
所以圆的过A点的切线方程为: .
.
(3)由题知,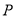 , B,
, B,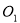 ,C四点共圆,
,C四点共圆,
设点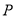 坐标为
坐标为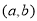 ,则
,则 , B,
, B,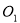 ,C四点所在圆的方程为
,C四点所在圆的方程为
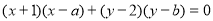 ,
,
与圆 联立,得直线
联立,得直线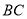 的方程为
的方程为 ,
,
又直线AM的方程为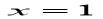 ,联立两直线方程, H点
,联立两直线方程, H点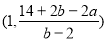 ,
,
所以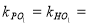
 ,又
,又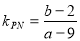 ,
,
所以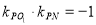 .
.
考点:圆的方程、切线方程以及圆的综合问题.


科目:高中数学 来源:2015届辽宁省大连市高三上学期期中考试理科数学试卷(解析版) 题型:选择题
已知 函数
函数 是偶函数,则
是偶函数,则 的图象与
的图象与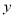 轴交点纵坐标的最小值为( )
轴交点纵坐标的最小值为( )
A. B.
B.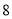 C.4 D.
C.4 D.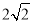
查看答案和解析>>
科目:高中数学 来源:2016届江苏省连云港市高一下学期期末数学试卷(三星)(解析版) 题型:解答题
一只不透明的袋子中装有颜色分别为红、黄、蓝、白的球各一个,这些球除颜色外都相同.
(1)求搅匀后从中任意摸出1个球,恰好是红球的概率;
(2)搅匀后从中任意摸出1个球,记录下颜色后放回袋子中并搅匀,再从中任意摸出1个球,求至少有一次摸出的球是红球的概率.
查看答案和解析>>
科目:高中数学 来源:2016届江苏省连云港市高一下学期期末数学试卷(三星)(解析版) 题型:填空题
在一次选拔运动员中,测得7名选手的身高(单位:cm)的茎叶图为: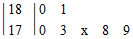 ,记录的平均身高为177 cm,有一名候选人的身高记录不清楚,其末位数记为x,那么x的值为 .
,记录的平均身高为177 cm,有一名候选人的身高记录不清楚,其末位数记为x,那么x的值为 .
查看答案和解析>>
科目:高中数学 来源:2015届青海省西宁市高三上学期第一次月考理科数学试卷(解析版) 题型:解答题
为迎接高一新生报到,学校向高三甲、乙、丙、丁四个实验班征召志愿者.统计如下:
班 级 | 甲 | 乙 | 丙 | 丁 |
志愿者人数 | 45 | 60 | 30 | 15 |
为了更进一步了解志愿者的来源,采用分层抽样的方法从上述四个班的志愿者中随机抽取50名参加问卷调查.
(1)从参加问卷调查的50名志愿者中随机抽取两名,求这两名来自同一个班级的概率;
(2)在参加问卷调查的50名志愿者中,从来自甲、丙两个班级的志愿者中随机抽取两名,用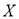 表示抽得甲班志愿者的人数,求
表示抽得甲班志愿者的人数,求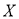 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com