
为迎接高一新生报到,学校向高三甲、乙、丙、丁四个实验班征召志愿者.统计如下:
班 级 | 甲 | 乙 | 丙 | 丁 |
志愿者人数 | 45 | 60 | 30 | 15 |
为了更进一步了解志愿者的来源,采用分层抽样的方法从上述四个班的志愿者中随机抽取50名参加问卷调查.
(1)从参加问卷调查的50名志愿者中随机抽取两名,求这两名来自同一个班级的概率;
(2)在参加问卷调查的50名志愿者中,从来自甲、丙两个班级的志愿者中随机抽取两名,用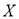 表示抽得甲班志愿者的人数,求
表示抽得甲班志愿者的人数,求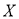 的分布列和数学期望.
的分布列和数学期望.
(1)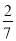 ;(2)详见解析.
;(2)详见解析.
【解析】
试题分析:(1)由已知得问卷调查中,从四个班级中抽取的人数分别为15,20,10,5,从参加问卷调查的50名志愿者中随机抽取两名的取法共有 种,这两名志愿者来自同一班级的取法共有
种,这两名志愿者来自同一班级的取法共有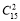 +
+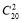 +
+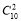 +
+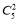 =350,由此能求出这两名来自同一个班级的概率.(2)由(1)知,在参加问卷调查的50名志愿者中,来自甲、丙两班的人员人数分别为15,10.X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和数学期望.
=350,由此能求出这两名来自同一个班级的概率.(2)由(1)知,在参加问卷调查的50名志愿者中,来自甲、丙两班的人员人数分别为15,10.X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和数学期望.
试题解析:【解析】
(1)由已知得问卷调查中,从四个班级中抽取的人数分别为15,20,10,5
2分
从参加问卷调查的50名志愿者中随机抽取两名的取法共有 种,
种,
这两名志愿者来自同一班级的取法共有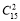 +
+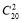 +
+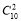 +
+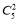 =350. 5分
=350. 5分
∴ . 6分
. 6分
(2)由(1)知,在参加问卷调查的50名志愿者中,来自甲、丙两班的人员人数分别为15,10.X的可能取值为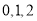 , 8分
, 8分
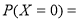
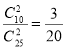 ,
, 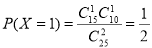 ,
, 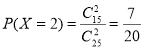 .
.
∴X的分布列为:
X |
|
|
|
|
|
|
|
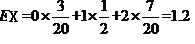 12分.
12分.
考点:1.离散型随机变量及其分布列;2.离散型随机变量的期望与方差.


科目:高中数学 来源:2016届江苏省连云港市高一下学期期末数学试卷(三星)(解析版) 题型:解答题
已知圆心在第二象限内,半径为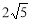 的圆
的圆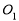 与
与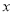 轴交于
轴交于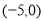 和
和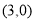 两点.
两点.
(1)求圆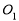 的方程;
的方程;
(2)求圆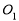 的过点A(1,6)的切线方程;
的过点A(1,6)的切线方程;
(3)已知点N(9,2)在(2)中的切线上,过点A作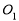 N的垂线,垂足为M,点H为线段AM上异于两个端点的动点,以点H为中点的弦与圆交于点B,C,过B,C两点分别作圆的切线,两切线交于点P,求直线
N的垂线,垂足为M,点H为线段AM上异于两个端点的动点,以点H为中点的弦与圆交于点B,C,过B,C两点分别作圆的切线,两切线交于点P,求直线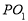 的斜率与直线PN的斜率之积.
的斜率与直线PN的斜率之积.

查看答案和解析>>
科目:高中数学 来源:2016届内蒙古高一下学期期末考试数学试卷(解析版) 题型:选择题
已知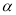 为第三象限角,则
为第三象限角,则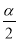 所在的象限是( )
所在的象限是( )
A.第一或第二象限 B.第二或第三象限
C.第一或第三象限 D.第二或第四象限
查看答案和解析>>
科目:高中数学 来源:2015届青海省西宁市高三上学期第一次月考理科数学试卷(解析版) 题型:填空题
如图,矩形OABC内的阴影部分由曲线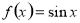 及直线
及直线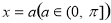 与
与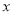 轴围成的区域,向矩形OABC内随机掷一点,该点落在阴影部分的概率为
轴围成的区域,向矩形OABC内随机掷一点,该点落在阴影部分的概率为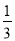 ,则
,则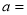 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com