


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
 和三棱锥
和三棱锥 组合而成,点
组合而成,点 、
、 、
、 在圆
在圆 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图4所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图4所示,其中 ,
, ,
, ,
, .
.
 ;
; 的体积.
的体积.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是 (写出所有正确命题的编号).
A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是 (写出所有正确命题的编号). 
 时,S为四边形;
时,S为四边形; 时,S为等腰梯形;
时,S为等腰梯形; 时,S与C1D1的交点R满足C1R=
时,S与C1D1的交点R满足C1R= ;
; <CQ<1时,S为六边形;
<CQ<1时,S为六边形; .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
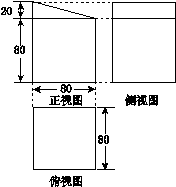
| A.40 000 cm2 | B.40 800 cm2 |
C.1600(22+ )cm2 )cm2 | D.41 600 cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com