
己知A、B、C分别为△ABC的三边a、b、c所对的角,向量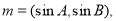
 ,且
,且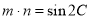 .
.
(1)求角C的大小:
(2)若sinA,sinC,sinB成等差数列,且 ,求边c的长.
,求边c的长.
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源:2013-2014学年天津市高考5月模拟文科数学试卷(解析版) 题型:选择题
10名工人某天生产同一零件,生产的件数是 设其平均数为
设其平均数为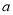 ,中位数为
,中位数为 ,众数为
,众数为 ,则有( )
,则有( )
A.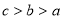 B.
B. C.
C.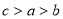 D.
D.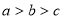
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市河北区高三总复习质量检测(一)理科数学试卷(解析版) 题型:选择题
已知函数 .那么不等式
.那么不等式 的解集为( ).
的解集为( ).
(A) (B)
(B)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市河北区高三总复习质量检测(一)文科数学试卷(解析版) 题型:解答题
已知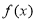 是二次函数,不等式
是二次函数,不等式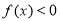 的解集是(0,5),且
的解集是(0,5),且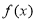 在区间[-1,4]上的最大值是12.
在区间[-1,4]上的最大值是12.
(1)求f(x)的解析式;
(2)是否存在正整数m,使得方程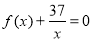 在区间
在区间 内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市河北区高三总复习质量检测(一)文科数学试卷(解析版) 题型:填空题
一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积为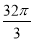 ,那么这个三棱柱的体积是_____________.
,那么这个三棱柱的体积是_____________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市河北区高三总复习质量检测(一)文科数学试卷(解析版) 题型:选择题
)执行右边的程序框图,输出m的值是( ).
(A)3 (B)4 (C)5 (D)6

查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市河东区高三一模试卷理科数学试卷(解析版) 题型:选择题
已知 ,且
,且 ,成等比数列,则xy( )
,成等比数列,则xy( )
A.有最大值e B.有最大值 C.有最小值e D.有最小值
C.有最小值e D.有最小值
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市河东区高三一模理科数学试卷(解析版) 题型:选择题
阅读图1的程序框图,该程序运行衍输出的k的值为( )

A.5 B.6 C.7 D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com