
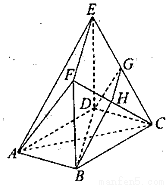
如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF 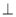 平面ABCD,BF=3,G、H分别是CE和CF的中点.
平面ABCD,BF=3,G、H分别是CE和CF的中点.
(Ⅰ)求证:AF//平面BDGH;
(Ⅱ)求 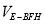
(Ⅰ)见解析(Ⅱ)1
【解析】
试题分析:(Ⅰ)连结AC、BD,设AC、BD交于O,连结HO,由ABCD为正方形知,O是AC的中点,由H是CF的中点及三角形中位线定理知,OH∥AF,由线面平行判定定理知,AF∥面BDGH;
(Ⅱ)由BDEF为矩形知DE⊥BD,由面BDEF⊥面ABCD及面面垂直性质定理知DE⊥面ABCD,所以DE⊥AC,由ABCD为正方形知AC⊥BD,所以AC⊥面BDEF,AO是A到面BDEF的距离,因为H是CF的中点,所以H到面BDEF的距离为AO的一半,很容易计算出棱锥H-BEF的体积就是棱锥E-BFH的体积.
试题解析:(Ⅰ) 证明:设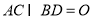 ,连接
,连接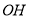 ,
,
在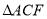 中,因为
中,因为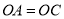 ,
,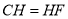 ,
,
所以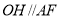 ,
,
又因为 平面
平面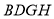 ,
,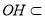 平面
平面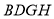 ,
,
所以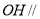 平面
平面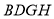 . (6分)
. (6分)
(Ⅱ)因为四边形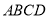 是正方形,
是正方形,
所以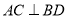 .
.
又因为平面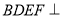 平面
平面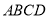 ,平面
,平面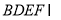 平面
平面 ,
,
且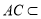 平面
平面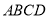 ,
,
所以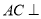 平面
平面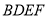 . 得
. 得 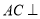 平面
平面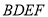 (8分)
(8分)
则H到平面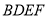 的距离为CO的一半
的距离为CO的一半
又因为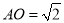 ,三角形
,三角形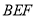 的面积
的面积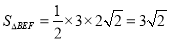 ,
,
所以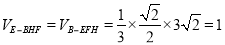 (12分)
(12分)
考点:线面平行的判定,面面垂直性质定理,线面垂直的判定与性质,锥体体积计算,推理论证能力


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2013-2014学年河南省原名校高三高考仿真模拟统一考试理科数学试卷(解析版) 题型:解答题
已知函数 
(Ⅰ)a=-3时,求不等式  的解集;
的解集;
(Ⅱ)若关于x的不等式  恒成立,求实数a的取值范围
恒成立,求实数a的取值范围
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省原名校高三高考仿真模拟统一考试理科数学试卷(解析版) 题型:选择题
设随机变量 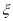 服从正态分布
服从正态分布 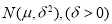 若
若 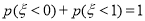 ,则
,则 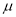 的值为
的值为
A.-1 B.l C.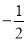 D.
D.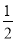
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省原名校高三高考仿真模拟统一考试文科数学试卷(解析版) 题型:解答题
已知 ,不等式
,不等式  的解集是
的解集是 
(Ⅰ)求a的值;
(Ⅱ)若  存在实数解,求实数
存在实数解,求实数  的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省邯郸市高三第二次模拟考试文科数学试卷(解析版) 题型:解答题
已知 、
、 为椭圆
为椭圆 的左右焦点,点
的左右焦点,点 为其上一点,且有
为其上一点,且有
 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)过 的直线
的直线 与椭圆
与椭圆 交于
交于 、
、 两点,过
两点,过 与
与 平行的直线
平行的直线 与椭圆
与椭圆 交于
交于 、
、 两点,求四边形
两点,求四边形 的面积
的面积 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com