若方程x2-11x+30+a=0两根都大于5,则实数a的取值范围是 .
【答案】
分析:根据x的方程x
2-11x+30+a=0两根都大于5可得:判别式大于等于0,,然后再由二根都大于5列出不等式即可解答.
解答:解:设方程x
2-11x+30+a=0两根为x
1,x
2,由于两根都大于5
故有(x
1-5)+(x
2-5)>0且(x
1-5)(x
2-5)>0
即x
1+x
2-10>0且x
1•x
2-5(x
1+x
2)+25>0
又由韦达定理可得:x
1+x
2=11,x
1x
2=30+a,
∴30+a-55+25>0,解得a>0,
又∵△=(-11)
2-4(30+a)≥0,解得:a
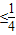
故实数a的取值范围是:(0,

]
故答案为:(0,

]
点评:本题考查根与系数的关系及根的判别式,关键是根据判别式及两根都大于5列出不等式,属基础题.

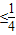
 ]
] ]
]
