
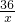 m,再将所用篱笆总长用含x的解析式来表示出来,最后利用基本不等式求出此函数的最小值及x取何值时取得最小值即得.
m,再将所用篱笆总长用含x的解析式来表示出来,最后利用基本不等式求出此函数的最小值及x取何值时取得最小值即得.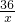 m,
m,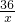 ),
),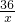 )≥4×6=24,当且仅当x=6时,取等号,
)≥4×6=24,当且仅当x=6时,取等号,

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源:学习高手必修一数学苏教版 苏教版 题型:044
如图所示,用一段长为20米的篱笆围成一个一边靠墙的矩形鸡圈ABCD,设AB=x,矩形ABCD的面积为S.
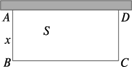
(1)求S关于x的函数解析式,并指明函数的定义域;
(2)求函数S(x)的值域;
(3)试问该函数有最小值吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com