
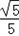 ,试求M的轨迹曲线C1的方程;
,试求M的轨迹曲线C1的方程;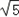 ,0)的直线m,使其与曲线C2交得弦|PQ|长度为8呢?
,0)的直线m,使其与曲线C2交得弦|PQ|长度为8呢?(1)∵定点A(1,0),定直线l:x=5,
动点M(x,y),M到点A的距离与M到直线l的距离之比为 ,
,
∴根据椭圆定义:M的轨迹为椭圆,其中c=1,e= =
= ,
,
∴a= ∴b=
∴b=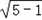 =2∴则C1轨迹方程为:
=2∴则C1轨迹方程为: .
.
(2)∵C1轨迹方程为: ,
,
∴C1的焦点为:(1,0),(﹣1,0),
C1的顶点为:( ,0),(﹣
,0),(﹣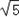 ,0)
,0)
由题意可知:C2为双曲线则a′=1,c'=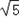 ,则b′=
,则b′= =2,
=2,
∴C2轨迹方程为:x2﹣ =1.
=1.
(3)当直线m的斜率不存在时,m的方程为:x=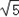 ,
,
它与C2:x2﹣ =1交于P(
=1交于P( ,﹣4)和Q(
,﹣4)和Q( ),得到得弦|PQ|=8.
),得到得弦|PQ|=8.
当直线m的斜率存在时,m的方程为y=k(x﹣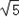 ),联立方程组
),联立方程组 ,
,
消去y,整理得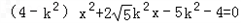 ,
,
设P(x1,y1),Q(x2,y2),则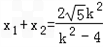 ,
,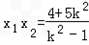 ,∴弦|PQ|长度为8,
,∴弦|PQ|长度为8,
∴ =8,解得k=
=8,解得k=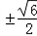 ,
,
∴直线m的方程为x= 或y=
或y=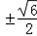 (x﹣
(x﹣ ).
).


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:
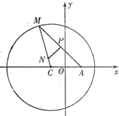 如图,已知定点A(1,0),定圆C:(x+1)2+y2=8,M为圆C上的一个动点,点P在线段AM上,点N在线段CM上,且满足
如图,已知定点A(1,0),定圆C:(x+1)2+y2=8,M为圆C上的一个动点,点P在线段AM上,点N在线段CM上,且满足| AM |
| AP |
| NP |
| AM |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ax |
| x+b |
| 2m |
| (x+1)|x-m| |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AE |
| AF |
| EP |
| OA |
| FO |
| OP |
| AM |
| AN |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com