
四个纪念币A、B、C、D,投掷时正面向上的概率如下表所示(0 < a < 1).
|
纪念币 |
A |
B |
C |
D |
|
概率 |
a |
a |
这四个纪念币同时投掷一次,设ξ表示出现正面向上的个数.
(1) 求ξ的分布列及数学期望;
(2) 在概率P (ξ= i ) (i = 0 , 1 , 2 , 3 , 4)中,若P (ξ= 2 )的值最大,求a的取值范围.
解:(1) P (ξ)是ξ个正面向上的概率,其中ξ的可能取值为0,1,2,3,4.
∴P (ξ=0) =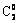 (1 - )2
(1 - )2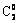 (1 - a)2 = (1 - a)2,
(1 - a)2 = (1 - a)2,
P (ξ=1) =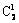 ·(1 - )
·(1 - )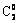 (1
- a)2 +
(1
- a)2 +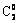 (1
- )2
(1
- )2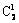 a(1 - a) = (1 - a)
a(1 - a) = (1 - a)
P (ξ=2)=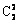 ·()2
·()2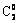 (1 - a)2 +
(1 - a)2 +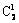 ·(1 - )
·(1 - )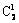 a(1
- a)
a(1
- a)
+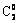 (1
- )2
(1
- )2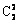 a2 = (1 + 2a - 2a2),
a2 = (1 + 2a - 2a2),
P (ξ=3) =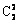 ·()2
·()2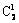 a(1 - a) +
a(1 - a) +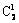 ·(1 - )
·(1 - )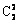 a2
= ,
a2
= ,
P (ξ=4) = 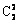 ()2
()2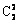 a2 = a2.
a2 = a2.
∴ξ的分布列为:
|
ξ |
0 |
1 |
2 |
3 |
4 |
|
P |
(1 - a)2 |
(1 - a) |
(1 + 2a - 2a2) |
a2 |
∴ξ的数学期望为:Eξ=0×(1- a)2+1×(1 - a)+ 2×(1 + 2a - 2a2)+ 3× +
4×a2 = 2a + 1. (7分)
(2) ∵0﹤a﹤1, ∴P (ξ=0) < P (ξ=1), P (ξ=4)﹤P (ξ=3)
则P (ξ=2) - P (ξ=1) = (1 + 2a - 2a2) - (1-a) = - (2a2- 4a+1)≥0
P (ξ=2) - P (ξ=3) = (1+2a-2a2)- = - (2a)≥0
由,得 ≤a≤,
即a的取值范围是[ , ]. (12分)


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
| 纪念币 | A | B | C | D | ||||
| 概率 |
|
|
a | a |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分12分)
四个纪念币A、B、C、D,投掷时正面向上的概率如下表所示(0<a<1)
| 纪念币 | A | B | C | D |
| 概率 | 1/2 | 1/2 | a | a |
这四个纪念币同时投掷一次,设ξ表示出正面向上的个数。
(1)求概率p(ξ)
(2)求在概率p(ξ),p(ξ=2)为最大时,a的取值范围。
(3)求ξ的数学期望。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省实验中学高三(上)第二次月考数学试卷(理科)(解析版) 题型:解答题
| 纪念币 | A | B | C | D |
| 概率 |  |  | a | a |
查看答案和解析>>
科目:高中数学 来源:2010年四川省成都市石室中学高考数学三模试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com