
选做题:请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题记分
22.(本小题满分10分)选修4—1几何证明选讲
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F。
(I)求证:DE是⊙O的切线;
(II)若 的值.
的值.

23.(本小题满分10分)选修4—2坐标系与参数方程
设直角坐标系原点与极坐标极点重合, x轴正半轴与极轴重合,若已知曲线C的极坐标方程为 ,点F1、F2为其左、右焦点,直线l的参数方程为
,点F1、F2为其左、右焦点,直线l的参数方程为
(I)求直线l的普通方程和曲线C的直角坐标方程;
(II)求曲线C上的动点P到直线l的最大距离。
24.(本小题满分10分)选修4—5不等式选讲
对于任意的实数 恒成立,记实数M的最大值是m。
恒成立,记实数M的最大值是m。
(1)求m的值;
(2)解不等式
略
【解析】22.(I)证明:连结OD,可得∠ODA=∠OAD=∠DAC …………2分
∴OD//AE 又AE⊥DE …………3分
∴OE⊥OD,又OD为半径
∴DE是的⊙O切线 …………5分
|
则有∠DOH=∠CAB
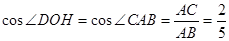 ………6分
………6分
设OD=5x,则AB=10x,OH=2x,
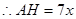 ………………7分
………………7分
由△AED≌△AHD可得AE=AH=7x ………8分
又由△AEF∽△DOF
可得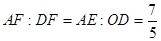
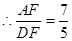 …………10分
…………10分
23.解:(I)直线l普通方程为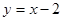 …………3分
…………3分
椭圆C的普通方程为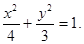 …………6分
…………6分
(II)由椭圆的普通方程可以得到其参数方程为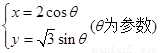
则动点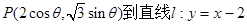 的距离为
的距离为
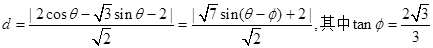 ………8分
………8分
由于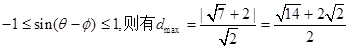 …………10分
…………10分
24.解:(I)不等式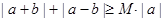 恒成立,
恒成立,
即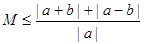 对于任意的实数
对于任意的实数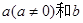 恒成立,
恒成立,
只要左边恒小于或等于右边的最小值。 …………2分
因为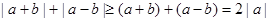 ,
,
当且仅当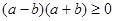 时等号成立,
时等号成立,
即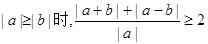 成立,
成立,
也就是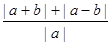 的最小值是2。 …………5分
的最小值是2。 …………5分
(2)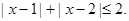 解法1:利用绝对值的意义得:
解法1:利用绝对值的意义得: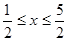
解法2:当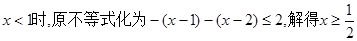 ,
,
所以x的取值范围是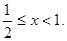
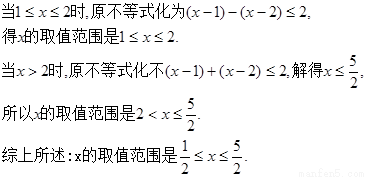
解法3:构造函数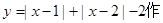
|
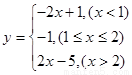 的图象,利用图象有
的图象,利用图象有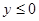 得:
得:
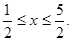 ………………10分
………………10分


科目:高中数学 来源: 题型:
 (2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)
(2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)
|
| a2 |
| x |
| b2 |
| y |
| (a+b)2 |
| x+y |
| a |
| x |
| b |
| y |
| 2 |
| x |
| 9 |
| 1-2x |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010年海南省高三五校联考数学(文) 题型:选择题
选做题:请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题记分
22.(本小题满分10分)选修4—1几何证明选讲
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F。
(I)求证:DE是⊙O的切线;
(II)若 的值.
的值.

23.(本小题满分10分)选修4—2坐标系与参数方程
设直角坐标系原点与极坐标极点重合, x轴正半轴与极轴重合,若已知曲线C的极坐标方程为 ,点F1、F2为其左、右焦点,直线l的参数方程为
,点F1、F2为其左、右焦点,直线l的参数方程为
(I)求直线l的普通方程和曲线C的直角坐标方程;
(II)求曲线C上的动点P到直线l的最大距离。
24.(本小题满分10分)选修4—5不等式选讲
对于任意的实数 恒成立,记实数M的最大值是m。
恒成立,记实数M的最大值是m。
(1)求m的值;
(2)解不等式
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)
选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)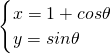 (θ为参数),求曲线C上的点到直线x-y+1=0的距离的最大值.
(θ为参数),求曲线C上的点到直线x-y+1=0的距离的最大值.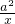 +
+ ≥
≥ ,当且仅当
,当且仅当 =
=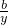 时上式取等号.请利用以上结论,求函数f(x)=
时上式取等号.请利用以上结论,求函数f(x)= +
+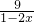 (x∈0,
(x∈0, )的最小值.
)的最小值.查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省十二校高三(下)4月联考数学试卷(理科)(解析版) 题型:解答题
 (θ为参数),求曲线C上的点到直线x-y+1=0的距离的最大值.
(θ为参数),求曲线C上的点到直线x-y+1=0的距离的最大值. +
+ ≥
≥ ,当且仅当
,当且仅当 =
= 时上式取等号.请利用以上结论,求函数f(x)=
时上式取等号.请利用以上结论,求函数f(x)= +
+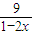 (x∈0,
(x∈0, )的最小值.
)的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com