
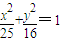 上的动点,F1,F2为椭圆的左、右焦点,则
上的动点,F1,F2为椭圆的左、右焦点,则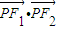 的最小值为 ,此时点P的坐标为 .
的最小值为 ,此时点P的坐标为 . 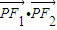 根据三角函数的性质求得最小值,进而可求得此时t的值,进而可得点P此时的坐标.
根据三角函数的性质求得最小值,进而可求得此时t的值,进而可得点P此时的坐标. =(-3-5cost,-4sint)•(3-5cost,-4sint)=25cos2t-9+16sin2t=9cos2t+7≥7.
=(-3-5cost,-4sint)•(3-5cost,-4sint)=25cos2t-9+16sin2t=9cos2t+7≥7.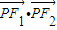 的最小值为7,则点P的坐标为(0,±4)
的最小值为7,则点P的坐标为(0,±4)

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
设直线l:2x+y+2=0关于原点对称的直线为l′,若l′与椭圆x2+![]() =1的交点为A、B,点P为椭圆上的动点,则使△PAB面积为
=1的交点为A、B,点P为椭圆上的动点,则使△PAB面积为![]() 的点P的个数为( )
的点P的个数为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com