
【题目】已知函数f(x)=ln(x+1)+ax2 , a>0.
(1)讨论函数f(x)的单调性;
(2)若函数f(x)在区间(﹣1,0)有唯一零点x0 , 证明: ![]() .
.
【答案】
(1)解: ![]() ,x>﹣1,
,x>﹣1,
令g(x)=2ax2+2ax+1,△=4a2﹣8a=4a(a﹣2),
若△<0,即0<a<2,则g(x)>0,
当x∈(﹣1,+∞)时,f'(x)>0,f(x)单调递增,
若△=0,即a=2,则g(x)≥0,仅当 ![]() 时,等号成立,
时,等号成立,
当x∈(﹣1,+∞)时,f'(x)≥0,f(x)单调递增.
若△>0,即a>2,则g(x)有两个零点 ![]() ,
, ![]() ,
,
由g(﹣1)=g(0)=1>0, ![]() 得
得 ![]() ,
,
当x∈(﹣1,x1)时,g(x)>0,f'(x)>0,f(x)单调递增;
当x∈(x1,x2)时,g(x)<0,f'(x)<0,f(x)单调递减;
当x∈(x2,+∞)时,g(x)>0,f'(x)>0,f(x)单调递增.
综上所述,
当0<a≤2时,f(x)在(﹣1,+∞)上单调递增;
当a>2时,f(x)在 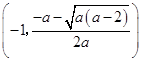 和
和 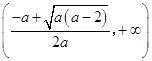 上单调递增,
上单调递增,
在 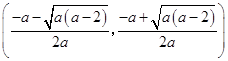 上单调递减.
上单调递减.
(2)解:由(1)及f(0)=0可知:仅当极大值等于零,即f(x1)=0时,符合要求.
此时,x1就是函数f(x)在区间(﹣1,0)的唯一零点x0.
所以 ![]() ,从而有
,从而有 ![]() ,
,
又因为 ![]() ,所以
,所以 ![]() ,
,
令x0+1=t,则 ![]() ,
,
设 ![]() ,则
,则 ![]() ,
,
再由(1)知: ![]() ,h'(t)<0,h(t)单调递减,
,h'(t)<0,h(t)单调递减,
又因为 ![]() ,
, ![]() ,
,
所以e﹣2<t<e﹣1,即 ![]() .
.
【解析】(1)求出函数的导数,通过讨论a的范围,求出函数的单调区间;(2)求出 ![]() ,得到
,得到 ![]() ,令x0+1=t,则
,令x0+1=t,则 ![]() ,设
,设 ![]() ,根据函数的单调性证明即可.
,根据函数的单调性证明即可.


科目:高中数学 来源: 题型:
【题目】已知各项均不相等的等差数列{an}的前四项和S4=14,且a1 , a3 , a7成等比数列. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设Tn为数列{ ![]() }的前n项和,若Tn≤λan+1对n∈N*恒成立,求实数λ的最小值.
}的前n项和,若Tn≤λan+1对n∈N*恒成立,求实数λ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD-A1B1C1D1为正方体,下面结论错误的是 ( )
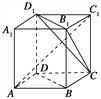
A. BD∥平面CB1D1 B. AC1⊥BD
C. AC1⊥平面CB1D1 D. 异面直线AD与CB1所成的角为60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=
∠ACD=90°,∠EAC=60°,AB=AC=AE.
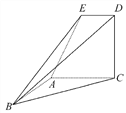
(1)在直线BC上是否存在一点P,使得DP∥平面EAB?请证明你的结论.
(2)求平面EBD与平面ABC所成的锐二面角θ的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,一个矩形花园里需要铺两条笔直的小路,已知矩形花园长AD=5m,宽AB=3m,其中一条小路定为AC,另一条小路过点D,问如何在BC上找到一点M,使得两条小路AC与DM相互垂直?
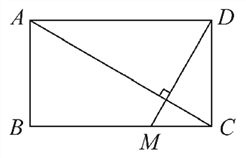
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P-ABCD的底面ABCD是正方形,E,F分别为AC和PB上的点,它的直观图,正视图,侧视图如图所示.
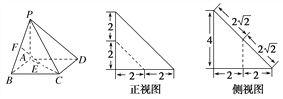
(1)求EF与平面ABCD所成角的大小;
(2)求二面角B-PA-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,给出以下四个结论:
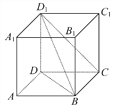
①D1C∥平面A1ABB1;②A1D1与平面BCD1相交;
③AD⊥平面D1DB;④平面BCD1⊥平面A1ABB1.
其中正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>0)的焦点在x轴上,且椭圆C的焦距为2. (Ⅰ)求椭圆C的标准方程;
=1(a>0)的焦点在x轴上,且椭圆C的焦距为2. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)过点R(4,0)的直线l与椭圆C交于两点P,Q,过P作PN⊥x轴且与椭圆C交于另一点N,F为椭圆C的右焦点,求证:三点N,F,Q在同一条直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com