
【题目】如图所示,一个矩形花园里需要铺两条笔直的小路,已知矩形花园长AD=5m,宽AB=3m,其中一条小路定为AC,另一条小路过点D,问如何在BC上找到一点M,使得两条小路AC与DM相互垂直?
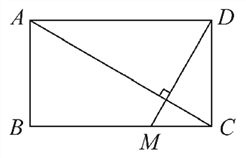
【答案】BM=3.2m时,两条小路AC与DM相互垂直.
【解析】试题分析:首先建立平面坐标系,以点B为坐标原点,BC,BA所在直线分别为x轴,y轴建立直角坐标系,由于长方形的长度均知道,故点坐标都是已知的设点M的坐标为(x,0),根据题意只需AC⊥DM,所以kAC·kDM=-1。列出方程,解出即可。
如图,以点B为坐标原点,BC,BA所在直线分别为x轴,y轴建立直角坐标系.
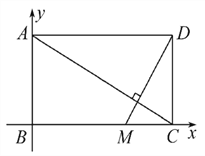
由AD=5m,AB=3m,可得C(5,0),D(5,3),A(0,3).
设点M的坐标为(x,0),
因为AC⊥DM,所以kAC·kDM=-1.
所以![]() ·
·![]() =-1,即x=
=-1,即x=![]() =3.2,即BM=3.2m时,两条小路AC与DM相互垂直.
=3.2,即BM=3.2m时,两条小路AC与DM相互垂直.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥PABC中,不能证明AP⊥BC的条件是( )

A. AP⊥PB,AP⊥PC
B. AP⊥PB,BC⊥PB
C. 平面BPC⊥平面APC,BC⊥PC
D. AP⊥平面PBC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AB=AA1=1,E为BC中点. 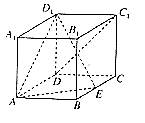
(1)求证:C1D⊥D1E;
(2)若二面角B1﹣AE﹣D1的大小为90°,求AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 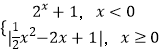 ,方程f2(x)﹣af(x)+b=0(b≠0)有六个不同的实数解,则3a+b的取值范围是( )
,方程f2(x)﹣af(x)+b=0(b≠0)有六个不同的实数解,则3a+b的取值范围是( )
A.[6,11]
B.[3,11]
C.(6,11)
D.(3,11)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(x+1)+ax2 , a>0.
(1)讨论函数f(x)的单调性;
(2)若函数f(x)在区间(﹣1,0)有唯一零点x0 , 证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,该几何体是由一个直三棱柱ADE﹣BCF和一个正四棱锥P﹣ABCD组合而成,AD⊥AF,AE=AD=2. (Ⅰ)证明:平面PAD⊥平面ABFE;
(Ⅱ)求正四棱锥P﹣ABCD的高h,使得二面角C﹣AF﹣P的余弦值是 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
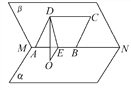
【题目】如图,已知二面角α-MN-β的大小为60°,菱形ABCD在平面β内,A,B两点在棱MN上,∠BAD=60°,E是AB的中点,DO⊥平面α,垂足为O.
(1)证明:AB⊥平面ODE.
(2)求异面直线BC与OD所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)判断函数![]() 的奇偶性,并给出证明;
的奇偶性,并给出证明;
(2)解不等式: ![]() ;
;
(3)若函数![]() 在
在![]() 上单调递减,比较f(2)+f(4)+…+f(2n)与2n(n∈N*)的大小关系,并说明理由.
上单调递减,比较f(2)+f(4)+…+f(2n)与2n(n∈N*)的大小关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com