
【题目】设函数f(x)=x(lnx﹣ax)(a∈R)在区间(0,2)上有两个极值点,则a的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:方法一:f(x)=x(lnx﹣ax),求导f′(x)=lnx﹣2ax+1,
由题意,关于x的方程a= ![]() 在区间(0,+∞)由两个不相等的实根,
在区间(0,+∞)由两个不相等的实根,
令h(x)= ![]() ,h′(x)=﹣
,h′(x)=﹣ ![]() ,
,
当x∈(0,1)时,h(x)单调递增,当x∈(1,+∞)单调递减,
当x→+∞时,h(x)→0,
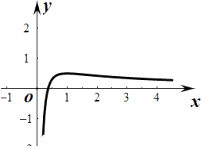
由图象可知:函数f(x)=x(lnx﹣ax),在(0,2)上由两个极值,
只需 ![]() <a<
<a< ![]() ,
,
故D.
方法二:f(x)=x(lnx﹣ax),求导f′(x)=lnx﹣2ax+1,
由题意,关于x的方程2ax=lnx+1在区间(0,2)由两个不相等的实根,
则y=2ax与y=lnx+1有两个交点,
由直线y=lnx+1,求导y′= ![]() ,
,
设切点(x0,y0), ![]() =
= ![]() ,解得:x0=1,
,解得:x0=1,
∴切线的斜率k=1,
则2a=1,a= ![]() ,
,
则当x=2,则直线斜率k= ![]() ,
,
则a= ![]() ,
,
∴a的取值范围( ![]() ,
, ![]() ),
),
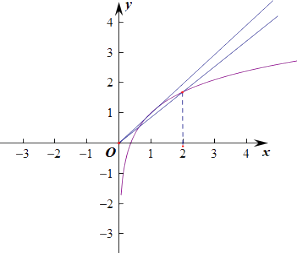
故选D.
方法一:求导f′(x)=lnx﹣2ax+1,由关于x的方程a= ![]() 在区间(0,+∞)由两个不相等的实根,构造辅助函数,根据函数单调性即可求得a取值范围;
在区间(0,+∞)由两个不相等的实根,构造辅助函数,根据函数单调性即可求得a取值范围;
方法二:由题意,关于x的方程2ax=lnx+1在区间(0,2)由两个不相等的实根,则y=2ax与y=lnx+1有两个交点,根据导数的几何意义,即可求得a的取值范围.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】如图,已知一艘海监船O上配有雷达,其监测范围是半径为25 km的圆形区域,一艘外籍轮船从位于海监船正东40 km的A处出发,径直驶向位于海监船正北30 km的B处岛屿,速度为28 km/h.
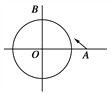
问:这艘外籍轮船能否被海监船监测到?若能,持续时间多长?(要求用坐标法)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣(2a+1)x+lnx(a∈R) (Ⅰ)当a>0时,求函数f(x)的单调区间;
(Ⅱ)设g(x)=f(x)+2ax,若g(x)有两个极值点x1 , x2 , 且不等式g(x1)+g(x2)<λ(x1+x2)恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,PA⊥平面ABC,AE⊥PB,AB⊥BC,AF⊥PC,PA=AB=BC.
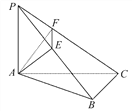
(1)求证:平面AEF⊥平面PBC.
(2)求二面角P-BC-A的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,一个矩形花园里需要铺两条笔直的小路,已知矩形花园长AD=5m,宽AB=3m,其中一条小路定为AC,另一条小路过点D,问如何在BC上找到一点M,使得两条小路AC与DM相互垂直?
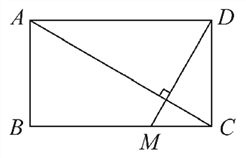
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(I)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(II)求证: ![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
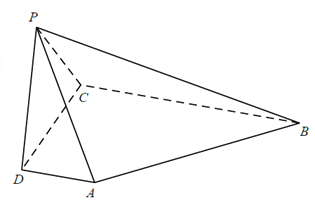
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年存节期间,某服装超市举办了一次有奖促销活动,消费每超过600 元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种. 方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸到2个红球,则打6折;若摸到1个红球,则打7折;若没摸到红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了 600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新学年伊始,某中学学生社团开始招新,某高一新生对“海济公益社”、“理科学社”、“高音低调乐社”很感兴趣,假设她能被这三个社团接受的概率分别为 ![]() ,
, ![]() ,
, ![]() .
.
(1)求此新生被两个社团接受的概率;
(2)设此新生最终参加的社团数为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com