
 的单调递增区间是
的单调递增区间是 ,+∞)
,+∞) )
) ,2)
,2) 的解析式,我们易判断出函数f(x)=
的解析式,我们易判断出函数f(x)= 的定义域为(-∞,-3)∪(2,+∞),将函数分析为t=x2+x-6,y=
的定义域为(-∞,-3)∪(2,+∞),将函数分析为t=x2+x-6,y=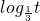 ,由于外函数在其定义域为恒为减函数,故求函数f(x)=
,由于外函数在其定义域为恒为减函数,故求函数f(x)= 的单调递增区间,即求内函数t=x2+x-6在定义域内的单调递减区间,由二次函数的性质,易得到答案.
的单调递增区间,即求内函数t=x2+x-6在定义域内的单调递减区间,由二次函数的性质,易得到答案. 的解析式有意义,自变量x须满足x2+x-6>0
的解析式有意义,自变量x须满足x2+x-6>0 的定义域为(-∞,-3)∪(2,+∞)
的定义域为(-∞,-3)∪(2,+∞)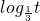
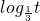 为减函数
为减函数 的单调递增区间是区间(-∞,-3)
的单调递增区间是区间(-∞,-3)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com