求“方程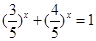
的解”有如下解题思路：设
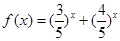，则
在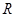
上单调递减，且
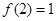，所以原方程有唯一解
．类比上述解题思路，方程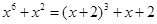
的解集为_ __ ．
科目：高中数学 来源： 题型：填空题
以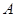
表示值域为R的函数组成的集合，
表示具有如下性质的函数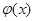
组成的集合：对于函数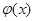，存在一个正数
，使得函数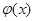的值域包含于区间
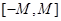。例如，当
，
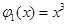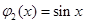时，
，
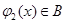.现有如下命题：
①设函数
的定义域为
，则“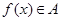
”的充要条件是“
，
，
”；
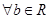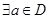②若学科网函数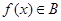
，则有最大值和最小值；
③若函数，
的定义域相同，且，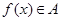
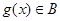，则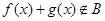
；
④若函数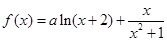
（
，
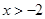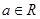）有最大值，则.
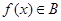其中的真命题有 .（写出所有真命题的序号）
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
给出定义：若函数f(x)在D上可导，即f′(x)存在，且导函数f′(x)在D上也可导，则称f(x)在D上存在二阶导函数，记f″(x)＝(f′(x))′，若f″(x)<0在D上恒成立，则称f(x)在D上为凸函数．以下四个函数在(0，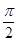
)上不是凸函数的是________．
①f(x)＝sim x＋cos x ②f(x)＝ln x－2x
③f(x)＝x3＋2x－1 ④f(x)＝x·ex
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，则解方程可得：
或
．若
，则
．
满足
，则
的值为 ．
的方程
有实根，则实数
的取值范围为________．
，方程
有五个不同的实数解时，
的取值范围为 ．
，若函数g(x)＝f(x)－k有两个零点，则实数k的取值范围是________．
在
单调递减，
.若
，则
的取值范围是__________.