
【题目】某工厂为了对新研究的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x元 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销售y件 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程 ![]() ,其中
,其中 ![]() =﹣20.
=﹣20.
(2)预计在今后的销售中,销售与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价定为多少元?
 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:
【题目】在下列结论中: ①函数y=sin(kπ﹣x)(k∈Z)为奇函数;
②函数 ![]() 的图象关于点
的图象关于点 ![]() 对称;
对称;
③函数 ![]() 的图象的一条对称轴为
的图象的一条对称轴为 ![]() π;
π;
④若tan(π﹣x)=2,则cos2x= ![]() .
.
其中正确结论的序号为(把所有正确结论的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() (
(![]() ),原点
),原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,其中:点
,其中:点![]() ,点
,点![]() .
.
(1)求该椭圆![]() 的离心率
的离心率![]() ;
;
(2)经过椭圆右焦点![]() 的直线
的直线![]() 和该椭圆交于
和该椭圆交于![]() 两点,点
两点,点![]() 在椭圆上,
在椭圆上, ![]() 为原点,若
为原点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题.他们在沙滩上画点或用小石子表示数,按照点或小石子能排列的形状对数进行分类.如下图中实心点的个数5,9,14,20,…为梯形数.根据图形的构成,记此数列的第2013项为a2013 , 则a2013﹣5=( ) 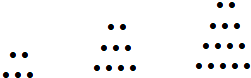
A.2019×2013
B.2019×2012
C.1006×2013
D.2019×1006
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】欧阳修《卖油翁)中写到:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌漓沥之,自钱孔入,而钱不湿”,可见“行行出状元”,卖油翁的技艺让人叹为观止,若铜钱是直径为4 cm的圆,中间有边长为l cm的正方形孔.若随机向铜钱上滴一滴油(设油滴整体落在铜钱上).则油滴(设油滴是直径为0.2 cm的球)正好落入孔中(油滴整体落入孔中)的概率是_________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体A1B1C1D1﹣ABCD中,AD=CD=4,AD1=5,M是线段B1D1的中点. 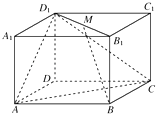
(1)求证:BM∥平面D1AC;
(2)求直线DD1与平面D1AC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)<0且f(﹣1)=0则不等式f(x)g(x)<0的解集为( )
A.(﹣1,0)∪(1,+∞)
B.(﹣1,0)∪(0,1)
C.(﹣∞,﹣1)∪(1,+∞)
D.(﹣∞,﹣1)∪(0,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com