
ĄžĚâÄżĄżÎŞÁË˝âČËĂÇśÔÓÚšúźŇĐ°䲟ľÄĄ°ÉúÓýśţĚĽˇĹżŞĄąŐţ˛ßľÄČȜȣŹĎÖÔÚÄłĘĐ˝řĐĐľ÷˛éŁŹËćťúłéľ÷ÁË50ČËŁŹËűĂÇÄęÁäľÄĆľĘýˇÖ˛źź°Ö§łÖĄ°ÉúÓýśţĚĽĄąČËĘýČçĎÂąíŁş
ÄęÁä | [5ŁŹ15ŁŠ | [15ŁŹ25ŁŠ | [25ŁŹ35ŁŠ | [35ŁŹ45ŁŠ | [45ŁŹ55ŁŠ | [55ŁŹ65ŁŠ |
ĆľĘý | 5 | 10 | 15 | 10 | 5 | 5 |
Ö§łÖĄ°ÉúÓýśţĚĽĄą | 4 | 5 | 12 | 8 | 2 | 1 |
Ł¨1ŁŠÓÉŇÔÉĎÍłźĆĘýžÝĚîĎÂĂć2ĄÁ2ÁĐÁŞąíŁť
ÄęÁ䲝ľÍÓÚ45ËęľÄČË | ÄęÁäľÍÓÚ45ËęľÄČË | şĎźĆ | |
Ö§łÖĄ°ÉúÓýśţĚĽĄą | a= | c= | |
˛ťÖ§łÖĄ°ÉúÓýśţĚĽĄą | b= | d= | |
şĎźĆ |
Ł¨2ŁŠĹĐśĎĘǡńÓĐ99%ľÄ°ŃÎŐČĎÎŞŇÔ45ËęÎŞˇÖ˝çľăśÔĄ°ÉúÓýśţĚĽˇĹżŞĄąŐţ˛ßľÄÖ§łÖśČÓвîŇ죎
PŁ¨K2ĄÝkŁŠ | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
¸˝ąíŁşK2= ![]() ŁŽ
ŁŽ

| Äęźś | ¸ßÖĐżÎłĚ | Äęźś | łőÖĐżÎłĚ |
| ¸ßŇť | ¸ßŇťĂâˇŃżÎłĚÍĆźöŁĄ | łőŇť | łőŇťĂâˇŃżÎłĚÍĆźöŁĄ |
| ¸ßśţ | ¸ßśţĂâˇŃżÎłĚÍĆźöŁĄ | łőśţ | łőśţĂâˇŃżÎłĚÍĆźöŁĄ |
| ¸ßČý | ¸ßČýĂâˇŃżÎłĚÍĆźöŁĄ | łőČý | łőČýĂâˇŃżÎłĚÍĆźöŁĄ |
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżÄłĐŁ´Ó˛ÎźÓ¸ßČýťŻŃ§ľĂˇÖŃľÁˇľÄѧÉúÖĐËćťúłéłö60ĂűѧÉúŁŹ˝ŤĆ䝯ѧłÉź¨Ł¨žůÎŞŐűĘýŁŠˇÖłÉÁůśÎ![]() Ą˘
Ą˘![]() Ą˘ĄĄ˘
Ą˘ĄĄ˘![]() şóľĂľ˝˛żˇÖĆľÂʡֲźÖąˇ˝ÍźŁ¨ČçÍźŁŠ.
şóľĂľ˝˛żˇÖĆľÂʡֲźÖąˇ˝ÍźŁ¨ČçÍźŁŠ.
šŰ˛ěÍźĐÎÖĐľÄĐĹϢŁŹťŘ´đĎÂÁĐÎĘĚ⣺
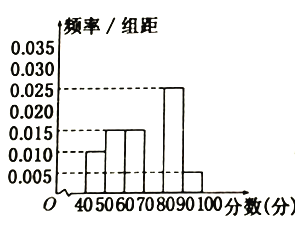
Ł¨1ŁŠÇóˇÖĘýÔÚ![]() ÄÚľÄĆľÂĘŁŹ˛˘˛šČŤĆľÂʡֲźÖąˇ˝ÍźŁť
ÄÚľÄĆľÂĘŁŹ˛˘˛šČŤĆľÂʡֲźÖąˇ˝ÍźŁť
Ł¨2ŁŠžÝ´ËšŔźĆąž´ÎżźĘÔľÄĆ˝žůˇÖŁť
Ł¨3ŁŠČô´Ó60ĂűѧÉúÖĐËćťúłéČĄ2ČËŁŹłéľ˝ľÄѧÉúłÉź¨ÔÚ![]() ÄÚźÇ0ˇÖŁŹÔÚ
ÄÚźÇ0ˇÖŁŹÔÚ![]() ÄÚźÇ1ˇÖŁŹÔÚ
ÄÚźÇ1ˇÖŁŹÔÚ![]() ÄÚźÇ2ˇÖŁŹÓĂ
ÄÚźÇ2ˇÖŁŹÓĂ![]() ąíĘžłéČĄ˝áĘřşóľÄ×ܟǡ֣ŹÇó
ąíĘžłéČĄ˝áĘřşóľÄ×ܟǡ֣ŹÇó![]() ľÄˇÖ˛źÁĐ.
ľÄˇÖ˛źÁĐ.
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżŇŃÖŞś¨ŇĺÔÚRÉϾĺŻĘýfŁ¨xŁŠ=2|xŠm|Š1Ł¨mÎŞĘľĘýŁŠÎŞĹźşŻĘýŁŹźÇa=fŁ¨log0.53ŁŠŁŹb=fŁ¨log25ŁŠŁŹc=fŁ¨2mŁŠŁŹÔňaŁŹbŁŹcľÄ´óĐĄšŘϾΪ ŁŽ
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżÉčĂüĚâ![]() ŁşĘľĘý
ŁşĘľĘý![]() Âú×ă
Âú×ă![]() ŁŹĆäÖĐ
ŁŹĆäÖĐ![]() ŁťĂüĚâ
ŁťĂüĚâ![]() ŁşĘľĘý
ŁşĘľĘý![]() Âú×ă
Âú×ă![]() .
.
Ł¨1ŁŠČô![]() ŁŹÇŇ
ŁŹÇŇ![]() ÎŞŐ棏ÇóĘľĘý
ÎŞŐ棏ÇóĘľĘý![]() ľÄČĄÖľˇśÎ§Łť
ľÄČĄÖľˇśÎ§Łť
Ł¨2ŁŠČô![]() ĘÇ
ĘÇ![]() ľÄłäˇÖ˛ťąŘŇŞĚőźţŁŹÇóĘľĘý
ľÄłäˇÖ˛ťąŘŇŞĚőźţŁŹÇóĘľĘý![]() ľÄČĄÖľˇśÎ§.
ľÄČĄÖľˇśÎ§.
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżÉčfŁ¨xŁŠ= ![]() Ł¨aŁž0ŁŹbŁž0ŁŠŁŽ
Ł¨aŁž0ŁŹbŁž0ŁŠŁŽ
Ł¨1ŁŠľąa=b=1ĘąŁŹÖ¤Ă÷ŁşfŁ¨xŁŠ˛ťĘÇĆ溯ĘýŁť
Ł¨2ŁŠÉčfŁ¨xŁŠĘÇĆ溯ĘýŁŹÇóaÓëbľÄÖľŁť
Ł¨3ŁŠÔÚŁ¨2ŁŠľÄĚőźţĎÂŁŹĘÔÖ¤Ă÷şŻĘýfŁ¨xŁŠľÄľĽľ÷ĐÔŁŹ˛˘˝â˛ťľČĘ˝fŁ¨1ŠmŁŠ+fŁ¨1+m2ŁŠŁź0ŁŽ
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżŇŃÖŞÄłÖĐѧ¸ßČýÎĿưŕѧÉúš˛ÓĐ![]() Č˲ΟÓÁËĘýѧÓëľŘŔíľÄËŽĆ˝˛âĘÔŁŹĎÖѧУžöś¨ŔűÓĂËćťúĘýąíˇ¨´ÓÖĐłéČĄ
Č˲ΟÓÁËĘýѧÓëľŘŔíľÄËŽĆ˝˛âĘÔŁŹĎÖѧУžöś¨ŔűÓĂËćťúĘýąíˇ¨´ÓÖĐłéČĄ![]() ČË˝řĐгɟ¨łéŃůÍłźĆŁŹĎČ˝Ť
ČË˝řĐгɟ¨łéŃůÍłźĆŁŹĎČ˝Ť![]() ČË°´
ČË°´![]() ˝řĐĐąŕşĹŁŽ
˝řĐĐąŕşĹŁŽ
Ł¨˘ńŁŠČçšű´ÓľÚ![]() ĐĐľÚ
ĐĐľÚ![]() ÁĐľÄĘýżŞĘźĎňÓŇśÁŁŹÇëÄăŇŔ´ÎĐ´łö×îĎČźě˛âľÄ
ÁĐľÄĘýżŞĘźĎňÓŇśÁŁŹÇëÄăŇŔ´ÎĐ´łö×îĎČźě˛âľÄ![]() ¸öČ˾ĹŕşĹŁťŁ¨ĎÂĂćŐŞČĄÁËľÚ
¸öČ˾ĹŕşĹŁťŁ¨ĎÂĂćŐŞČĄÁËľÚ![]() ĐĐ ÖÁľÚ
ĐĐ ÖÁľÚ![]() ĐĐŁŠ
ĐĐŁŠ

Ł¨˘ňŁŠłéľÄ![]() ČËľÄĘýѧÓëľŘŔíľÄËŽĆ˝˛âĘԳɟ¨ČçĎÂąíŁş
ČËľÄĘýѧÓëľŘŔíľÄËŽĆ˝˛âĘԳɟ¨ČçĎÂąíŁş
ČËĘý | Ęýѧ | |||
ÓĹĐă | ÁźşĂ | ź°¸ń | ||
ľŘ Ŕí | ÓĹĐă | 7 | 20 | 5 |
ÁźşĂ | 9 | 18 | 6 | |
ź°¸ń |
| 4 |
| |
łÉź¨ˇÖÎŞÓĹĐ㥢ÁźşĂĄ˘ź°¸ńČý¸öľČźśŁŹşáĎňĄ˘×ÝĎňˇÖąđąíĘžľŘŔíłÉź¨ÓëĘýѧłÉź¨ŁŹŔýČ磺ąíÖĐĘýѧłÉź¨ÎŞÁźşĂľÄš˛ÓĐ![]() ČËŁŹČôÔÚ¸ĂŃůąžÖĐŁŹĘýѧłÉź¨ÓĹĐăÂĘÎŞ
ČËŁŹČôÔÚ¸ĂŃůąžÖĐŁŹĘýѧłÉź¨ÓĹĐăÂĘÎŞ![]() ŁŹÇó
ŁŹÇó![]() ľÄÖľŁŽ
ľÄÖľŁŽ
Ł¨˘óŁŠ˝Ť![]() ľÄ
ľÄ![]() ąíĘžłÉÓĐĐňĘýśÔ
ąíĘžłÉÓĐĐňĘýśÔ![]() ŁŹÇóĄ°ÔÚľŘŔíłÉź¨ÎŞź°¸ńľÄѧÉúÖĐŁŹĘýѧłÉź¨ÎŞÓĹĐăľÄČËĘýąČź°¸ńľÄČËĘýÉŮĄąľÄĘýśÔ
ŁŹÇóĄ°ÔÚľŘŔíłÉź¨ÎŞź°¸ńľÄѧÉúÖĐŁŹĘýѧłÉź¨ÎŞÓĹĐăľÄČËĘýąČź°¸ńľÄČËĘýÉŮĄąľÄĘýśÔ![]() ľÄ¸ĹÂĘŁŽ
ľÄ¸ĹÂĘŁŽ
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżŇŃÖŞśţ´ÎşŻĘýfŁ¨xŁŠÂú×ăfŁ¨0ŁŠ=2şÍfŁ¨x+1ŁŠŠfŁ¨xŁŠ=2xŠ1śÔČÎŇâĘľĘýxśźłÉÁ˘ŁŽ
Ł¨1ŁŠÇóşŻĘýfŁ¨xŁŠľÄ˝âÎöĘ˝Łť
Ł¨2ŁŠľątĄĘ[Š1ŁŹ3]ĘąŁŹÇóy=fŁ¨2tŁŠľÄÖľÓňŁŽ
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżÄłŃ§ĐŁśÔź×Ą˘ŇŇÁ˝¸ö°ŕźś˝řĐĐÁËÎďŔí˛âŃ飏łÉź¨ÍłźĆČçĎÂŁ¨Ăż°ŕ50ČËŁŠŁş
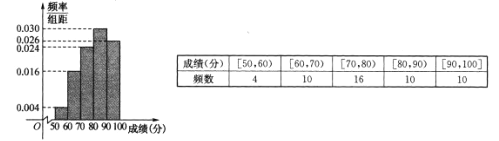
Ł¨1ŁŠšŔźĆź×°ŕľÄĆ˝žůłÉź¨Łť
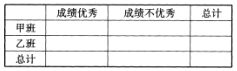
Ł¨2ŁŠłÉź¨˛ťľÍÓÚ80ˇÖźÇÎŞĄ°ÓĹĐ㥹.ÇëÍęłÉĎÂĂćľÄ![]() ÁĐÁŞąíŁŹ˛˘ĹĐśĎĘǡńÓĐ85%ľÄ°ŃÎŐČĎÎŞŁşĄ°łÉź¨ÓĹĐ㥹ÓëËůÔÚ˝Ěѧ°ŕźśÓКأż
ÁĐÁŞąíŁŹ˛˘ĹĐśĎĘǡńÓĐ85%ľÄ°ŃÎŐČĎÎŞŁşĄ°łÉź¨ÓĹĐ㥹ÓëËůÔÚ˝Ěѧ°ŕźśÓКأż
Ł¨3ŁŠ´ÓÁ˝¸ö°ŕźśŁŹłÉź¨ÔÚ![]() ľÄѧÉúÖĐČÎŃĄ2ČËŁŹźÇĘÂźţ
ľÄѧÉúÖĐČÎŃĄ2ČËŁŹźÇĘÂźţ![]() ÎŞĄ°ŃĄłöľÄ2ČËÖĐÇĄÓĐ1ČËŔ´×ԟװॹ.ÇóĘÂźţ
ÎŞĄ°ŃĄłöľÄ2ČËÖĐÇĄÓĐ1ČËŔ´×ԟװॹ.ÇóĘÂźţ![]() ľÄ¸ĹÂĘ
ľÄ¸ĹÂĘ![]() .
.
¸˝Łş 
![]()
˛éż´´đ°¸şÍ˝âÎö>>
šúźĘѧУÓĹŃĄ - ÁˇĎ°˛áÁĐąí - ĘÔĚâÁĐąí
şţąąĘĄťĽÁŞÍřÎĽˇ¨şÍ˛ťÁźĐĹϢžŮą¨Ć˝Ě¨ | ÍřÉĎÓĐşŚĐĹϢžŮą¨×¨Çř | ľçĐĹՊƞٹ¨×¨Çř | ÉćŔúʡĐéÎŢÖ÷ŇĺÓĐşŚĐĹϢžŮą¨×¨Çř | ÉćĆóÇÖȨžŮą¨×¨Çř
ÎĽˇ¨şÍ˛ťÁźĐĹϢžŮą¨ľçť°Łş027-86699610 žŮą¨ÓĘĎ䣺58377363@163.com