
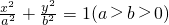 上任一点P到两个焦点的距离的和为
上任一点P到两个焦点的距离的和为 ,P与椭圆长轴两顶点连线的斜率之积为
,P与椭圆长轴两顶点连线的斜率之积为 .设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2).
.设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2).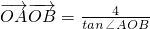 (O为坐标原点),求|y1-y2|的值;
(O为坐标原点),求|y1-y2|的值; ,又
,又 ,∴b2=2,c2=a2-b2=1.
,∴b2=2,c2=a2-b2=1. .
.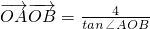 ,∴
,∴ ,
, ,
, ,
, ,故|y1-y2|=4.
,故|y1-y2|=4.
 .
. ,
, ;由P与椭圆长轴两顶点连线的斜率之积为
;由P与椭圆长轴两顶点连线的斜率之积为 ,可得
,可得 ,即可得到a,b2.
,即可得到a,b2.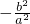 、直线QA、QB的倾斜角互为补角?kQA+kQB=0、直线与椭圆的方程相交问题转化为一元二次方程的根与系数的关系、斜率计算公式等是解题的关键.
、直线QA、QB的倾斜角互为补角?kQA+kQB=0、直线与椭圆的方程相交问题转化为一元二次方程的根与系数的关系、斜率计算公式等是解题的关键. 

 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 3 |
| OA |
| OB |
| 4 |
| tan∠AOB |
查看答案和解析>>
科目:高中数学 来源:黑龙江省哈尔滨市第六中学2011届高三第一次模拟考试数学试题(理工类) 题型:044
已知椭圆![]() (a>b>0)的左、右焦点分别为F1,F2,A为椭圆短轴的一个顶点,且
(a>b>0)的左、右焦点分别为F1,F2,A为椭圆短轴的一个顶点,且![]() 是直角三角形,椭圆上任一点P到左焦点F1的距离的最大值为
是直角三角形,椭圆上任一点P到左焦点F1的距离的最大值为![]()
(1)求椭圆C的方程;
(2)与两坐标轴都不垂直的直线l:![]() 交椭圆C于E,F两点,且以线段EF为直径的圆恒过坐标原点,当△OEF面积的最大值时,求直线l的方程.
交椭圆C于E,F两点,且以线段EF为直径的圆恒过坐标原点,当△OEF面积的最大值时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源:2011年黑龙江省哈尔滨六中高考数学一模试卷(理科)(解析版) 题型:解答题
 (a>b>0)的左、右焦点分别为F1,F2,A为椭圆短轴的一个顶点,且△AF1F2是直角三角形,椭圆上任一点P到左焦点F1的距离的最大值为
(a>b>0)的左、右焦点分别为F1,F2,A为椭圆短轴的一个顶点,且△AF1F2是直角三角形,椭圆上任一点P到左焦点F1的距离的最大值为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com