
已知函数 ,
, .
.
(1)求函数 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)已知 中的三个内角
中的三个内角 所对的边分别为
所对的边分别为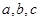 ,若锐角
,若锐角 满足
满足 ,且
,且 ,
, ,求
,求 的面积.
的面积.
(1)最小正周期为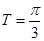 ,单调递减区间是
,单调递减区间是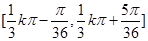 ,
,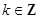 ;
;
(2)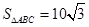 .
.
解析试题分析:(1)首先应用三角函数公式,化简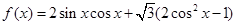 得到
得到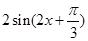 ,从而得到
,从而得到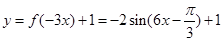
其最小正周期为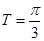 ,由复合函数的单调性,由
,由复合函数的单调性,由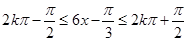 解得,
解得,
函数 的单调递减区间是
的单调递减区间是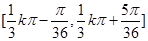 ,
,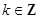 ;
;
(2)由已知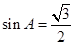 ,根据
,根据 ,求得
,求得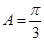 .
.
由正弦定理可得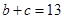 ;
;
应用余弦定理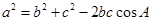 得:
得: ,
,
求得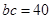 ,应用三角形面积计算公式即可得解.
,应用三角形面积计算公式即可得解.
解得本题,巧妙地利用“整体观”,确定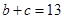 及
及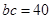 ,简化了解题过程.
,简化了解题过程.
试题解析:(1)
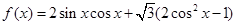
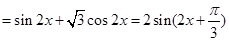 2分
2分
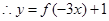 的最小正周期为
的最小正周期为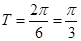 3分
3分
由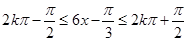 得:
得: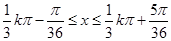 ,
,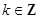 ,
, 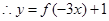 的单调递减区间是
的单调递减区间是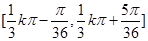 ,
,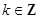 6分
6分
(2)∵ ,∴
,∴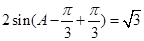 ,∴
,∴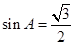 7分
7分
∵ ,∴
,∴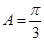 .由正弦定理得:
.由正弦定理得: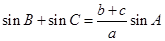 ,
,
即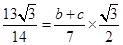 ,∴
,∴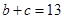 9分
9分
由余弦定理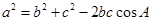 得:
得: ,
,
即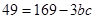 ,∴
,∴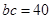 11分
11分
∴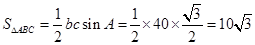 12分
12分
考点:三角函数式的化简,三角函数的性质,正弦、余弦定理的应用,三角形面积公式.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:解答题
如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计, 可以使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 中,
中, 的对边分别为
的对边分别为 且
且 .
.
(1)判断△ 的形状,并求
的形状,并求 的取值范围;
的取值范围;
(2)如图,三角形 的顶点
的顶点 分别在
分别在 上运动,
上运动, ,若直线
,若直线 直线
直线 ,且相交于点
,且相交于点 ,求
,求 间距离的取值范围.
间距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某人沿一条折线段组成的小路前进,从 到
到 ,方位角(从正北方向顺时针转到
,方位角(从正北方向顺时针转到 方向所成的角)是
方向所成的角)是 ,距离是3km;从
,距离是3km;从 到
到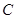 ,方位角是110°,距离是3km;从
,方位角是110°,距离是3km;从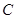 到
到 ,方位角是140°,距离是(
,方位角是140°,距离是( )km.试画出大致示意图,并计算出从A到D的方位角和距离(结果保留根号).
)km.试画出大致示意图,并计算出从A到D的方位角和距离(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com