
若数列![]() 的前
的前![]() 项和
项和![]() 是
是![]() 二项展开式中各项系数的和
二项展开式中各项系数的和![]() .
.
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)若数列![]() 满足
满足![]() ,且
,且![]()
![]() ,求数列
,求数列![]() 的通
的通
项及其前![]() 项和
项和![]() ;
;
(III)求证:![]() .
.
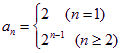 ,
,![]()
解:(Ⅰ)由题意![]() , -----------------------------------------------------2分
, -----------------------------------------------------2分
![]() ,
,
两式相减得![]() . --------------------3分
. --------------------3分
当![]() 时,
时,![]() ,
,
∴ . --------------------------------------------------4分
. --------------------------------------------------4分
(Ⅱ)∵![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
………
![]() .
.
以上各式相加得
![]() .
.
∵![]() ,
,
∴![]() . -----------------------------------------------------------------6分
. -----------------------------------------------------------------6分
∴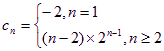 . -------------------------------------------------7分
. -------------------------------------------------7分
∴![]() ,
,
∴![]() .
.
∴![]() .
.
![]()
=![]() .
.
∴![]() . -------------------------------------------------------------9分
. -------------------------------------------------------------9分
(3)![]() =
=![]()
![]()
![]()
=4+![]()
![]()
![]()
![]()
![]()
![]()
=![]()
![]()
![]()
![]()
![]() . -------------------------------------------12分
. -------------------------------------------12分
∵![]() , ∴ 需证明
, ∴ 需证明![]() ,用数学归纳法证明如下:
,用数学归纳法证明如下:
①当![]() 时,
时,![]() 成立.
成立.
②假设![]() 时,命题成立即
时,命题成立即![]() ,
,
那么,当![]() 时,
时,![]() 成立.
成立.
由①、②可得,对于![]() 都有
都有![]() 成立.
成立.
∴![]()
![]()
![]() .
.
∴![]() .---------------------------------------------------------------------------13分
.---------------------------------------------------------------------------13分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
(09年崇文区期末理)(13分)
若数列![]() 的前
的前![]() 项和
项和![]() 是
是![]() 二项展开式中各项系数的和
二项展开式中各项系数的和![]() .
.
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)若数列![]() 满足
满足![]() ,且
,且![]()
![]() ,求数列
,求数列![]() 的通
的通
项及其前![]() 项和
项和![]() ;
;
查看答案和解析>>
科目:高中数学 来源:2011届广西柳铁一中高三第二次月考文科数学卷 题型:解答题
若数列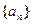 的前
的前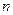 项和
项和 是
是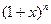 二项展开式中各项系数的和
二项展开式中各项系数的和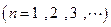 .
.
(Ⅰ)求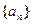 的通项公式;
的通项公式;
(Ⅱ)若数列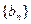 满足
满足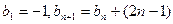 ,且
,且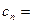
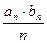 ,求数列
,求数列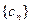 的通项及其前
的通项及其前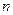 项和
项和 。
。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广西柳铁一中高三第二次月考文科数学卷 题型:解答题
若数列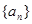 的前
的前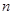 项和
项和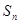 是
是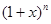 二项展开式中各项系数的和
二项展开式中各项系数的和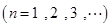 .
.
(Ⅰ)求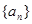 的通项公式;
的通项公式;
(Ⅱ)若数列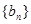 满足
满足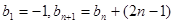 ,且
,且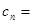
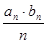 ,求数列
,求数列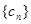 的通项及其前
的通项及其前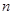 项和
项和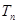 。
。
查看答案和解析>>
科目:高中数学 来源:2010年河北省高三押题数学(理)试题 题型:解答题
(本小题满分12分)
若数列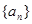 的前
的前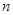 项和
项和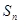 是
是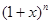 二项展开式中各项系数的和
二项展开式中各项系数的和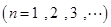 .
.
(Ⅰ)求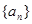 的通项公式;
的通项公式;
(Ⅱ)若数列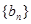 满足
满足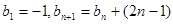 ,且
,且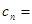
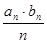 ,求数列
,求数列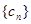 的通项及其前
的通项及其前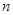 项和
项和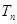 ;
;
(III)求证: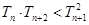 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com