练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知x、y为正实数，且满足关系式x2-2x+4y2=0，求x·y的最大值.

    思路分析：题中有两个变量x和y，首先应选择一个主要变量，将x、y表示为某一变量（x或y或其他变量）的函数关系，实现问题的转化，同时根据题设条件确定变量的取值范围，再利用导数（或均值不等式等）求函数的最大值.

    ?解：4y2=2x-x2，

    ∵y＞0，?

    ∴y=，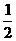

    ∴x·y=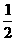x.?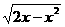

    由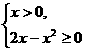

    解得0＜x≤2.

    设f（x）=xy=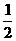x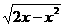（0＜x≤2）.?

    当0＜x＜2时，f′（x）=［+］=.?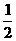

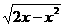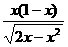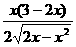    〔注：（）′=〕?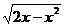

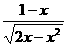    令f′（x）=0，得x=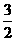或x=0（舍）.?

    ∴f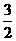（）=，又f（2）=0，?

    ∴函数f（x）的最大值为.?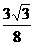

    即x·y的最大值为.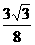

    温馨提示

    解决有关单调性和最值问题，导数是非常方便而且重要的工具.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知x，y为正实数，且2x+3y=1，则
    1
    x
    +
    1
    y
    的最小值为
    5+2
    		6
    5+2
    		6
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知x，y为正实数，则（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知x、y为正实数，满足2x+8y+9=xy，则xy的最小值为
    81
    81
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知x，y为正实数，且满足4x+3y=12，则xy的最大值为
    3
    3
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知x，y为正实数，且2x+y=1，则
    2
    x
    +
    1
    y
    的最小值是
    9
    9
    ．

    查看答案和解析>>

    同步练习册答案