
科目:高中数学 来源:不详 题型:解答题
| | 偏瘦 | 正常 | 肥胖 |
| 女生(人) | 100 | 173 | 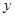 |
| 男生(人) |  | 177 | 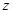 |
 的值;
的值;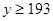 ,
,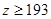 ,肥胖学生中男生不少于女生的概率。
,肥胖学生中男生不少于女生的概率。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
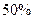 的企业抽查评估,评出优秀、良好、合格和不合格四个等次,
的企业抽查评估,评出优秀、良好、合格和不合格四个等次,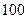 万元改造,由于自身技术原因,
万元改造,由于自身技术原因,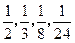 ,且由此增加的产值分别为
,且由此增加的产值分别为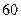 万元、
万元、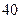 万元、
万元、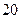 万元、
万元、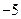 万元.设该企业当年因改造而增加利润为
万元.设该企业当年因改造而增加利润为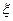 .
.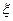 的数学期望.
的数学期望.| 评估得分 |  |  | 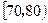 | 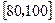 |
| 评定等级 | 不合格 | 合格 | 良好 | 优秀 |
| 奖惩(万元) | 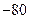 |  | 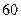 | 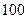 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.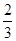 | B.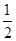 | C. | D.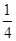 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 若干名学生组建数学奥林匹克集训队,要求选拔过程分前后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔相互独立。根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三
若干名学生组建数学奥林匹克集训队,要求选拔过程分前后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔相互独立。根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三 人合格的概率依次为0.5、0.6、0.4,第二次选拔,甲、乙、丙三人合格的概率依次为0.6、0.5、0.5。
人合格的概率依次为0.5、0.6、0.4,第二次选拔,甲、乙、丙三人合格的概率依次为0.6、0.5、0.5。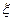 ,求
,求
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
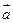 与向量
与向量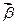 ,其满足
,其满足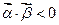 的概率是 ( )
的概率是 ( )A.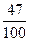 | B.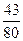 | C.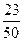 | D.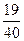 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com