考点:利用导数研究函数的极值
专题:计算题,导数的综合应用
分析:(Ⅰ)求出函数的导数,讨论a>0,a<0的单调区间和极大值,从而解得a的值;
(Ⅱ)求出函数的导数,讨论a>0,a<0时,区间[-2,0]的单调性,求出最大值,由条件只要令它小于
,即可得到a的范围.
解答:
解:(Ⅰ)函数f(x)=ax(x-2)
2(x∈R)的导数为f′(x)=a(x-2)(3x-2),
当a>0时,f′(x)>0得x>2或x<
,
f′(x)<0得
<x<2,则x=
取极大值,
即有
=32,解得a=27,成立;
当a<0时,f′(x)<0得x>2或x<
,f′(x)>0得
<x<2,
则x=2取极大值,
即有0=32,显然不成立.
故a=27;
(Ⅱ)函数f(x)=ax(x-2)
2(x∈R)的导数为f′(x)=a(x-2)(3x-2),
当a>0时,[-2,0]为增区间,即有f(0)最大且为0;
当a<0时,[-2,0]为减区间,即有f(-2)最大且为-32a;
对任意x∈[-2,0],不等式f(x)<
恒成立等价为
对任意x∈[-2,0],不等式f(x)
max<
恒成立,
当a>0时,有0<
成立;当a<0时,-32a<
,即a>-
.
故实数a的取值范围是:(-
,0)∪(0,+∞).
点评:本题考查导数的运用:求极值和单调区间,考查函数的单调性及运用:求最值,考查分类讨论的思想方法,以及运算能力,属于中档题.



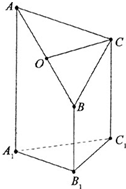 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=l,∠AlBlC1=90°,AAl=4,BBl=2,CCl=3,且设点O是AB的中点.
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=l,∠AlBlC1=90°,AAl=4,BBl=2,CCl=3,且设点O是AB的中点.