
 ,
, 且满足
且满足 .
.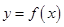 的解析式;
的解析式;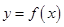 的最小正周期、最值及其对应的
的最小正周期、最值及其对应的 值;
值; 中,若
中,若 ,且
,且 ,
, ,求
,求 的长.
的长.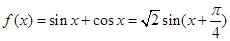 ;
; ,
,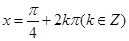 时,
时, 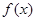 的最大值为
的最大值为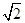 ,
,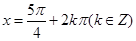 时,
时,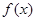 的最小值为
的最小值为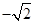 ;(3)
;(3) 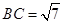 。
。 可求出f(x),然后再根据
可求出f(x),然后再根据 ,
, ,所以其周期为
,所以其周期为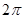 ,
,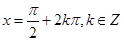 时,取得最大值1;当
时,取得最大值1;当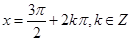 时,取得最小值-1,求出f(x)的最值.
时,取得最小值-1,求出f(x)的最值. ,求出A角,再利用余弦定理求出BC.
,求出A角,再利用余弦定理求出BC.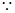
 且
且
 ·······1分
·······1分
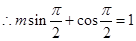
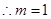 ·······3分
·······3分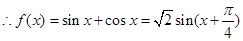 ·······5分
·······5分 ·······6分
·······6分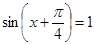 ,即
,即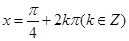 时,
时, 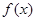 的最大值为
的最大值为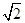 ,
,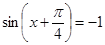 ,即
,即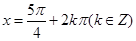 时,
时,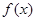 的最小值为
的最小值为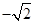 ·······8分
·······8分 , 即
, 即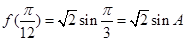
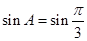 ·······9分
·······9分 是锐角
是锐角 的内角, ∴
的内角, ∴ ······10分
······10分 ,
,
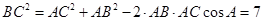 ······13分
······13分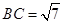 ·······14分
·······14分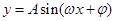 的周期及最值,三角方程,解三角形.
的周期及最值,三角方程,解三角形.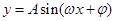 的周期及最值的求法是求解本题的关键,知道什么情况下适用正弦定理及余弦定理是求解第三问的基础.
的周期及最值的求法是求解本题的关键,知道什么情况下适用正弦定理及余弦定理是求解第三问的基础.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com