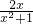练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    求函数f（x）=数学公式-2的极值．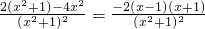

    解：由于函数f（x）的定义域为R
    f'（x）=
    令f'（x）=0得x=-1或x=1列表：
    x（-∞，-1）-1（-1，1）1（1，∞）
    f'（x）-0+0-
    f（x）↘极小值↗极大值↘
    由上表可以得到
    当x∈（-∞，-1）和x∈（1，+∞）时函数为减函数
    当x∈（-1，1）时，函数为增函数
    所以当x=-1时函数有极小值为-3；当x=1时函数有极大值为-1
    分析：由题意对函数求导，然后解f′（x）=0方程，得到x=-1或x=1，将（-∞，+∞）分为三个区间，最后通过列表得出导数在这三个区间的符号，讨论出函数的单调性，即可得出函数的最大最小值．
    点评：本题考查了函数的求导及极值的概念，其基本思路是利用导函数的零点求出可能的极值点，再利用表格讨论导数的正负，从而求其单调区间，最后得出函数的极值，这是典型的化归思想．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知向量
    a
    =(sinx，
    3
    2
    )    ，
    b
    =(cosx，-1)
    （1）当向量
    a
    与向量
    b
    共线时，求tanx的值；
    （2）求函数f（x）=2（
    a
    +
    b
    ）•
    b
    的最大值，并求函数取得最大值时的x的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=2|x-1|-3|x|．
    （1）画出函数f（x）的图象；
    （2）根据图象求函数f（x）=2|x-1|-3|x|的最大值；
    （3）根据图象解不等式f（x）＜0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2010•衢州一模）已知向量
    a
    =（sinx，
    3
    2
    ），
    b
    =（cosx，-1）．
    （I）当向量
    a
    与向量
    b
    共线时，求tanx的值；
    （II）求函数f（x）=2（
    a
    +
    b
    ）•
    b
    图象的一个对称中心的坐标．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年福建省南平市邵武一中高三（上）期末数学试卷（理科）（解析版） 题型：解答题

    已知向量=（cosx，sinx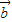），=（-cosx，cosx）
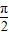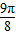    （1）当x∈[，]时，求函数f（x）=2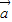•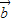+1的最大值．
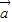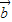    （2）设f（x）=2•+1，将函数y=f（x）的图象向右平移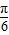个单位后，再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到函数y=g（x）的图象，求y=g（x）的单调递减区间．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年广东省汕头市四校高三联考数学试卷（文科）（解析版） 题型：解答题

    已知向量，
    （1）当向量与向量共线时，求tanx的值；
    （2）求函数f（x）=2（）的最大值，并求函数取得最大值时的x的值．

    查看答案和解析>>

    同步练习册答案