Question

（8分）已知f（x）的定义域为（0，＋∞），且满足f（2）＝1，f（xy）＝f（x）＋f（y），又当x2>x1>0时，f（x2）>f（x1）．

（1）求f（1）、f（4）、f（8）的值； （2）若有f（x）＋f（x－2）≤3成立，求x的取值范围．

 

Answer 1

（1）f（1）=0，f（4）=2，f（8）=3；（2）（2，4]

【解析】

试题分析：（1）令x=y=1可求出f（1）=0，令x=y=2可求出f（4）=2，令x=2，y=4，可求出f（8）=3；（2）由（1）可知f（8）=3，令y=x-2可得f（x）+f（x-2）=f[x（x-2）]，又因为对于函数f（x）有x2>x1>0时f（x2）>f（x1）即f（x）在（0，＋∞）上为增函数，所以不等式可化为，解得.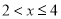

试题解析：（1）f（1）＝f（1）＋f（1），∴f（1）＝0，

f（4）＝f（2）＋f（2）＝1＋1＝2，

f（8）＝f（2）＋f（4）＝2＋1＝3.

∵f（x）＋f（x－2）≤3，∴f[x（x－2）]≤f（8），

又∵对于函数f（x）有x2>x1>0时f（x2）>f（x1），∴f（x）在（0，＋∞）上为增函数．

∴⇒2<x≤4. ∴x的取值范围为（2,4]．

考点：抽象函数的单调性及其应用