练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

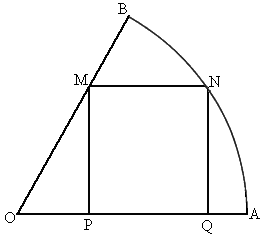
    如图，在半径为R的扇形OAB中，圆心角∠AOB=60°，在扇形中有一个内接矩形，求内接矩形的最大面积．

    答案：略
    解析：

    解：如题图，设PQ=x，MP=y，则矩形面积S=xy．连结ON，令∠AON=q ，则NQ=Rsinq (0°＜q ＜60°)，对△ONM，由正弦定理有

    ，∴，故

    ，当2q －60°=0°，即q =30°时，，

    ∴所求内接矩形的面积最大值为．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：学习周报　数学　北师大课标高一版(必修4)　2009－2010学年　第40期　总196期 北师大课标版 题型：044

    扇子在美观设计上，可以考虑用料、图案和形状，若从数学角度看，则认为符合黄金分割比例的扇子最美丽．如图，设纸扇半径为r，张开角为，要使纸扇面积与半径为r，圆心角为2π－的扇形面积的比为黄金分割比0.618，则纸扇的张开角应为多少度？(精确到10°)

    查看答案和解析>>

    同步练习册答案