
【题目】维生素C又叫抗坏血酸,是一种水溶性维生素,是高等灵长类动物与其他少数生物的必需营养素.维生素C虽不直接构成脑组织,也不向脑提供活动能源,但维生素C有多种健脑强身的功效,它是脑功能极为重要的营养物.维生素C的毒性很小,但食用过多仍可产生一些不良反应.根据食物中维C的含量可大致分为:含量很丰富:鲜枣、沙棘、猕猴桃、柚子,每100克中的维生素C含量超过100毫克;比较丰富:青椒、桂圆、番茄、草莓、甘蓝、黄瓜、柑橘、菜花,每100克中维生素C含量超过50毫克;相对丰富:白菜、油菜、香菜、菠菜、芹菜、苋菜、菜苔、豌豆、豇豆、萝卜,每100克中维生素C含量超过30~50毫克.现从猕猴桃、柚子两种食物中测得每100克所含维生素C的量(单位:![]() )得到茎叶图如图所示,则下列说法中不正确的是( )
)得到茎叶图如图所示,则下列说法中不正确的是( )
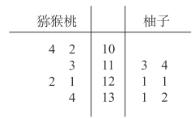
A.猕猴桃的平均数小于柚子的平均数
B.猕猴桃的方差小于柚子的方差
C.猕猴桃的极差为32
D.柚子的中位数为121
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,底面
,底面![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 中点,点
中点,点![]() 在线段
在线段![]() 上.
上.
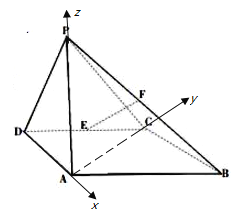
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]()
![]()
![]()
![]() ,求实数
,求实数![]() 使直线
使直线![]() 与平面
与平面![]() 所成角和直线
所成角和直线![]() 与平面
与平面![]() 所成角相等.
所成角相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 轴不重合,交圆
轴不重合,交圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() .
.
(1)求![]() 的值;
的值;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,与直线
两点,与直线![]() 相交于
相交于![]() 点,试问在椭圆
点,试问在椭圆![]() 上是否存在一定点
上是否存在一定点![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差数列(其中
成等差数列(其中![]() ,
,![]() ,
,![]() 分别指直线
分别指直线![]() ,
,![]() ,
,![]() 的斜率).若存在,求出
的斜率).若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科学家在研究物体的热辐射能力时定义了一个理想模型叫“黑体”,即一种能完全吸收照在其表面的电磁波(光)的物体.然后,黑体根据其本身特性再向周边辐射电磁波,科学研究发现单位面积的黑体向空间辐射的电磁波的功率![]() 与该黑体的绝对温度
与该黑体的绝对温度![]() 的
的![]() 次方成正比,即
次方成正比,即![]() ,
,![]() 为玻尔兹曼常数.而我们在做实验数据处理的过程中,往往不用基础变量作为横纵坐标,以本实验结果为例,
为玻尔兹曼常数.而我们在做实验数据处理的过程中,往往不用基础变量作为横纵坐标,以本实验结果为例,![]() 为纵坐标,以
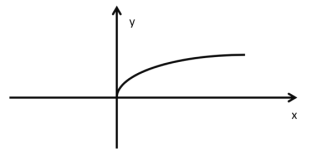
为纵坐标,以![]() 为横坐标,则能够近似得到______(曲线形状),那么如果继续研究该实验,若实验结果的曲线如图所示,试写出其可能的横纵坐标的变量形式______.
为横坐标,则能够近似得到______(曲线形状),那么如果继续研究该实验,若实验结果的曲线如图所示,试写出其可能的横纵坐标的变量形式______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与
与![]() ,
,![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() ,若点
,若点![]() 在曲线
在曲线![]() 位于第一象限的图象上运动,求四边形
位于第一象限的图象上运动,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“割圆术”是刘徽最突出的数学成就之一,他在《九章算术注》中提出割圆术,并作为计算圆的周长,面积已经圆周率的基础,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和3.1416这两个近似数值,这个结果是当时世界上圆周率计算的最精确数据.如图,当分割到圆内接正六边形时,某同学利用计算机随机模拟法向圆内随机投掷点,计算得出该点落在正六边形内的频率为0.8269,那么通过该实验计算出来的圆周率近似值为(参考数据:![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冠状病毒是一个大型病毒家族,已知可引起感冒以及中东呼吸综合征(MERS)和严重急性呼吸综合征(SARS)等较严重疾病.而今年出现在湖北武汉的新型冠状病毒(nCoV)是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状发热咳嗽气促和呼吸困难等.在较严重病例中,感染可导致肺炎严重急性呼吸综合征肾衰竭,甚至死亡.某医院为筛查冠状病毒,需要检验血液是否为阳性,现有![]() 份血液样本,有以下两种检验方式:
份血液样本,有以下两种检验方式:
方式一:逐份检验,则需要检验n次.
方式二:混合检验,将其中![]() 且k≥2)份血液样本分别取样混合在一起检验.若检验结果为阴性,这k份的血液全为阴性,因而这k份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份再逐份检验,此时这k份血液的检验次数总共为k+1.
且k≥2)份血液样本分别取样混合在一起检验.若检验结果为阴性,这k份的血液全为阴性,因而这k份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份再逐份检验,此时这k份血液的检验次数总共为k+1.
假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为p(0<p<1).现取其中![]() 且k≥2)份血液样本,记采用逐份检验,方式,样本需要检验的总次数为
且k≥2)份血液样本,记采用逐份检验,方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() .
.
(1)若![]() ,试求p关于k的函数关系式p=f(k).
,试求p关于k的函数关系式p=f(k).
(2)若p与干扰素计量![]() 相关,其中
相关,其中![]() 2)是不同的正实数,满足x1=1且
2)是不同的正实数,满足x1=1且![]() .
.
(i)求证:数列![]() 为等比数列;
为等比数列;
(ii)当![]() 时采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数的期望值更少,求k的最大值.
时采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数的期望值更少,求k的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com