
【题目】如图所示,四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,底面
,底面![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 中点,点
中点,点![]() 在线段
在线段![]() 上.
上.
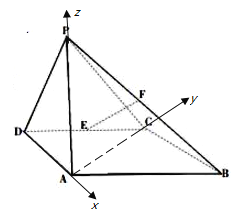
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]()
![]()
![]()
![]() ,求实数
,求实数![]() 使直线
使直线![]() 与平面
与平面![]() 所成角和直线
所成角和直线![]() 与平面
与平面![]() 所成角相等.
所成角相等.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列判断正确的是( )
A.线性回归直线![]() 必经过点
必经过点![]() ,
,![]() ,…
,…![]() 中心点
中心点![]()
B.从独立性检验可知有99%的把握认为吃地沟油与患胃肠癌有关系时,我们就说如果某人吃地沟油,那么他有99%可能患胃肠癌
C.若两个随机变量的线性相关性越强,则相关系数![]() 的绝对值越接近于1
的绝对值越接近于1
D.将一组数据的每一个数据都加上或减去同一个常数后,其方差也要加上或减去这个常数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两支围棋队各5名队员按事先排好的顺序进行擂台赛,双方1号队员先赛,负者被淘汰;然后负方的2号队员再与对方的胜者比赛,负者又被淘汰.依次类推,直到有一方队员全部被淘汰,则宣布另一方获胜.假设每名队员的实力相当,则比赛结束时甲队未上场队员数![]() 的数学期望
的数学期望![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年12月18日上午10时,在人民大会堂举行了庆祝改革开放40周年大会.40年众志成城,40年砥砺奋进,40年春风化雨,中国人民用双手书写了国家和民族发展的壮丽史诗.会后,央视媒体平台,收到了来自全国各地的纪念改革开放40年变化的老照片,并从众多照片中抽取了100张照片参加“改革开放40年图片展”,其作者年龄集中在![]() 之间,根据统计结果,做出频率分布直方图如下:
之间,根据统计结果,做出频率分布直方图如下:

(Ⅰ)求这100位作者年龄的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(Ⅱ)由频率分布直方图可以认为,作者年龄X服从正态分布![]() ,其中
,其中![]() 近似为样本平
近似为样本平
均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)利用该正态分布,求![]() ;
;
(ii)央视媒体平台从年龄在![]() 和
和![]() 的作者中,按照分层抽样的方法,抽出了7人参加“纪念改革开放40年图片展”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间
的作者中,按照分层抽样的方法,抽出了7人参加“纪念改革开放40年图片展”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间![]() 的人数是Y,求变量Y的分布列和数学期望.附:
的人数是Y,求变量Y的分布列和数学期望.附:![]() ,若
,若![]() ,则
,则![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”,彰显出中国式创新的强劲活力.某移动支付公司从某市移动支付用户中随机抽取100人进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 10 | 8 | 7 | 3 | 2 | 15 |
女 | 5 | 4 | 6 | 4 | 6 | 30 |
总计 | 15 | 12 | 13 | 7 | 8 | 45 |
(1)把每周使用移动支付6次及以上的用户称为“移动支付达人”,按分层抽样的方法,从参与调查的“移动支付达人”中,随机抽取6人,求抽取的6人中,男、女用户各多少人;
(2)把每周使用移动支付超过3次的用户称为“移动支付活跃用户”,根据表格中的数据完成下列![]() 列联表,问:能否有
列联表,问:能否有![]() 的把握认为“移动支付活跃用户”与性别有关?
的把握认为“移动支付活跃用户”与性别有关?
非移动支付活跃用户 | 移动支付活跃用户 | 总计 | |
男 | |||
女 | |||
总计 |
附参照表:
| 0.10 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
参考公式: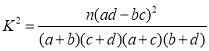 ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级有400名学生参加某项体育测试,根据男女学生人数比例,使用分层抽样的方法从中抽取了100名学生,记录他们的分数,将数据分成7组:![]() ,整理得到如下频率分布直方图:
,整理得到如下频率分布直方图:
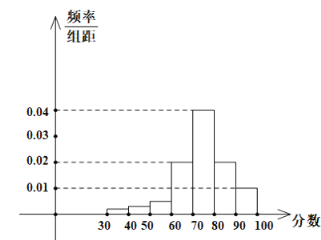
(1)若该样本中男生有55人,试估计该学校高三年级女生总人数;
(2)若规定小于60分为“不及格”,从该学校高三年级学生中随机抽取一人,估计该学生不及格的概率;
(3)若规定分数在![]() 为“良好”,
为“良好”,![]() 为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年12月份,我国湖北武汉出现了新型冠状病毒,人感染后会出现发热、咳嗽、气促和呼吸困难等,严重的可导致肺炎甚至危及生命.为了增强居民防护意识,增加居民防护知识,某居委会利用网络举办社区线上预防新冠肺炎知识答题比赛,所有居民都参与了防护知识网上答卷,最终甲、乙两人得分最高进入决赛,该社区设计了一个决赛方案:①甲、乙两人各自从![]() 个问题中随机抽
个问题中随机抽![]() 个.已知这
个.已知这![]() 个问题中,甲能正确回答其中的
个问题中,甲能正确回答其中的![]() 个,而乙能正确回答每个问题的概率均为
个,而乙能正确回答每个问题的概率均为![]() ,甲、乙两人对每个问题的回答相互独立、互不影响;②答对题目个数多的人获胜,若两人答对题目数相同,则由乙再从剩下的
,甲、乙两人对每个问题的回答相互独立、互不影响;②答对题目个数多的人获胜,若两人答对题目数相同,则由乙再从剩下的![]() 道题中选一道作答,答对则判乙胜,答错则判甲胜.
道题中选一道作答,答对则判乙胜,答错则判甲胜.
(1)求甲、乙两人共答对![]() 个问题的概率;
个问题的概率;
(2)试判断甲、乙谁更有可能获胜?并说明理由;
(3)求乙答对题目数的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com