
【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”,彰显出中国式创新的强劲活力.某移动支付公司从某市移动支付用户中随机抽取100人进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 10 | 8 | 7 | 3 | 2 | 15 |
女 | 5 | 4 | 6 | 4 | 6 | 30 |
总计 | 15 | 12 | 13 | 7 | 8 | 45 |
(1)把每周使用移动支付6次及以上的用户称为“移动支付达人”,按分层抽样的方法,从参与调查的“移动支付达人”中,随机抽取6人,求抽取的6人中,男、女用户各多少人;
(2)把每周使用移动支付超过3次的用户称为“移动支付活跃用户”,根据表格中的数据完成下列![]() 列联表,问:能否有
列联表,问:能否有![]() 的把握认为“移动支付活跃用户”与性别有关?
的把握认为“移动支付活跃用户”与性别有关?
非移动支付活跃用户 | 移动支付活跃用户 | 总计 | |
男 | |||
女 | |||
总计 |
附参照表:
| 0.10 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
参考公式: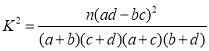 ,其中
,其中![]()
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源: 题型:
【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按![]() 元/度收费,超过200度但不超过400度的部分按
元/度收费,超过200度但不超过400度的部分按![]() 元/度收费,超过400度的部分按1.0元/度收费.
元/度收费,超过400度的部分按1.0元/度收费.

(Ⅰ)求某户居民用电费用![]() (单位:元)关于月用电量
(单位:元)关于月用电量![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(Ⅱ)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的占![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(Ⅲ)在满足(Ⅱ)的条件下,若以这100户居民用电量的频率代替该月全市居民用户用电量的概率,且同组中的数据用该组区间的中点代替,记![]() 为该居民用户1月份的用电费用,求
为该居民用户1月份的用电费用,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某大型活动中,甲、乙等五名志愿者被随机地分到A,B,C,D四个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求甲、乙两人同时参加A岗位服务的概率;
(2)求甲、乙两人不在同一个岗位服务的概率;
(3)求五名志愿者中仅有一人参加A岗位服务的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,底面
,底面![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 中点,点
中点,点![]() 在线段
在线段![]() 上.
上.
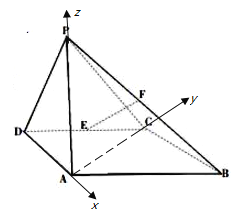
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]()
![]()
![]()
![]() ,求实数
,求实数![]() 使直线
使直线![]() 与平面
与平面![]() 所成角和直线
所成角和直线![]() 与平面
与平面![]() 所成角相等.
所成角相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个说法,其中正确的说法是( )
A.残差点分布的带状区域的宽度越窄相关指数越小;
B.在刻画回归模型的拟合效果时,相关指数![]() 的值越大,说明拟合的效果越好;
的值越大,说明拟合的效果越好;
C.在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均增加0.2个单位;
平均增加0.2个单位;
D.对分类变量![]() 与
与![]() ,若它们的随机变量
,若它们的随机变量![]() 的观测值
的观测值![]() 越小,则判断“
越小,则判断“![]() 与
与![]() 有关系”的把握程度越大.
有关系”的把握程度越大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经观测,某昆虫的产卵数![]() 与温度
与温度![]() 有关,现将收集到的温度
有关,现将收集到的温度![]() 和产卵数
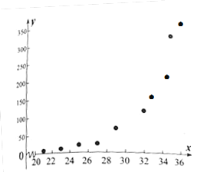
和产卵数![]() 的10组观测数据作了初步处理,得到如图的散点图及一些统计量表.
的10组观测数据作了初步处理,得到如图的散点图及一些统计量表.
|
|
|
|
|
|
275 | 731.1 | 21.7 | 150 | 2368.36 | 30 |
表中![]() ,
,![]()
(1)根据散点图判断,![]() ,
,![]() 与
与![]() 哪一个适宜作为
哪一个适宜作为![]() 与
与![]() 之间的回归方程模型?(给出判断即可,不必说明理由)
之间的回归方程模型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据.
①试求![]() 关于
关于![]() 回归方程;
回归方程;
②已知用人工培养该昆虫的成本![]() 与温度
与温度![]() 和产卵数
和产卵数![]() 的关系为
的关系为![]() ,当温度
,当温度![]() (
(![]() 取整数)为何值时,培养成本的预报值最小?
取整数)为何值时,培养成本的预报值最小?
附:对于一组数据![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为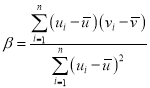 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:
满足:![]() ,当
,当![]() ,
,![]() 时.
时.
![]() 其中
其中![]() 表示
表示![]() ,
,![]() ,
,![]() ,
,![]() 中的最大项
中的最大项![]() ,有以下结论:
,有以下结论:
![]() 若数列
若数列![]() 是常数列,则
是常数列,则![]()
![]() 若数列
若数列![]() 是公差
是公差![]() 的等差数列,则
的等差数列,则![]() ;
;
![]() 若数列
若数列![]() 是公比为q的等比数列,则
是公比为q的等比数列,则![]()
则其中正确的结论是______![]() 写出所有正确结论的序号
写出所有正确结论的序号![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在新型冠状病毒疫情期间,商业活动受到很大影响某小型零售连锁店总部统计了本地区50家加盟店2月份的零售情况,统计数据如图所示.据估计,平均销售收入比去年同期下降40%,则去年2月份这50家加盟店的平均销售收入约为( )
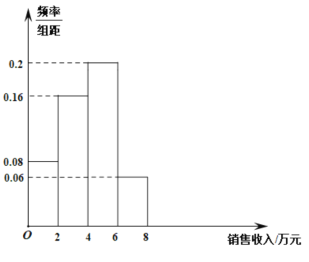
A.6.6万元B.3.96万元C.9.9万元D.7.92万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com