
����Ŀ��ij��Ϊ�˹��������Լ�õ磬ʵ�С�����ʽ����ۣ�������ÿ����������õ�������Ϊ���������õ���������200�ȵIJ��ְ�![]() Ԫ/���շѣ�����200�ȵ�������400�ȵIJ��ְ�
Ԫ/���շѣ�����200�ȵ�������400�ȵIJ��ְ�![]() Ԫ/���շѣ�����400�ȵIJ��ְ�1.0Ԫ/���շѣ�
Ԫ/���շѣ�����400�ȵIJ��ְ�1.0Ԫ/���շѣ�

������ij�������õ����![]() ����λ��Ԫ���������õ���
����λ��Ԫ���������õ���![]() ����λ���ȣ��ĺ�������ʽ��
����λ���ȣ��ĺ�������ʽ��
����Ϊ���˽������õ������ͨ������������˽���1�·�100������ÿ�����õ�����ͳ�Ʒ�����õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ������100�������У�����1�·��õ���ò�����260Ԫ��ռ![]() ����
����![]() ��
�� ![]() ��ֵ��
��ֵ��
���������㣨�������£�������100�������õ�����Ƶ�ʴ������ȫ�о����û��õ����ĸ��ʣ���ͬ���е������ø���������е���棬��![]() Ϊ�þ����û�1�·ݵ��õ���ã���
Ϊ�þ����û�1�·ݵ��õ���ã���![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
���𰸡���1�� ����2��
����2��![]() ��
�� ![]() ����3��������.
����3��������.
���������������: ��1����������ֶα�ʾ����������ʽ;��2����![]() ���루1���к�������ʽ�ɵ�
���루1���к�������ʽ�ɵ�![]() ����
����![]() ������Ƶ�ʷֲ�ֱ��ͼ�ɷֱ�õ�����
������Ƶ�ʷֲ�ֱ��ͼ�ɷֱ�õ�����![]() �ķ���,���ɵ�
�ķ���,���ɵ�![]() ;��3��
;��3��![]() ȡÿ���е�ֵ��Ϊ�������õ���,�ֱ������Ӧ�ķ���
ȡÿ���е�ֵ��Ϊ�������õ���,�ֱ������Ӧ�ķ���![]() ֵ,��Ӧ�ó�ÿ���ѵĸ���,���ɵõ�
ֵ,��Ӧ�ó�ÿ���ѵĸ���,���ɵõ�![]() �ĸ��ʷֲ���,Ȼ�����
�ĸ��ʷֲ���,Ȼ�����![]() ������.
������.
�������:��1����![]() ʱ��
ʱ�� ![]() ��
��
����![]() ʱ��
ʱ�� ![]() ��
��
����![]() ʱ��
ʱ�� ![]() ������
������![]() ��
��![]() ֮��ĺ�������ʽΪ
֮��ĺ�������ʽΪ
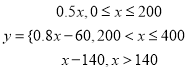 .
.
��2���ɣ�1����֪����![]() ʱ��
ʱ�� ![]() ����
����![]() �����Ƶ�ʷֲ�ֱ��ͼ��֪
�����Ƶ�ʷֲ�ֱ��ͼ��֪
![]() ����
����![]() ��
�� ![]()
��3���������֪![]() ��ȡ50��150��250��350��450��550��
��ȡ50��150��250��350��450��550��
��![]() ʱ��
ʱ�� ![]() ����
����![]() ��
��
��![]() ʱ��
ʱ�� ![]() ����
����![]() ��
��
��![]() ʱ��
ʱ�� ![]() ����
����![]() ��
��
��![]() ʱ��
ʱ�� ![]() ����
����![]() ��
��
��![]() ʱ��
ʱ�� ![]() ����
����![]() ��
��
��![]() ʱ��
ʱ�� ![]() ����
����![]() ��
��
��![]() �ĸ��ʷֲ���Ϊ
�ĸ��ʷֲ���Ϊ
| 25 | 75 | 140 | 220 | 310 | 410 |
| 0.1 | 0.2 | 0.3 | 0.2 | 0.15 | 0.05 |
�����������![]() ����ѧ����
����ѧ����
![]()


 Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
Happy holiday���ּ��������ҵ�㶫���������ϵ�д� ���������������Բ��������ϵ�д�
���������������Բ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯�� ![]() ������M=[a��b]������a��b������N={y|y=f��x����x��M}����ʹM=N������ʵ���ԣ�a��b��������
������M=[a��b]������a��b������N={y|y=f��x����x��M}����ʹM=N������ʵ���ԣ�a��b��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������M={x|��2��x��2}��N={y|0��y��2}�����������ĸ�ͼ�Σ������ܱ�ʾ��MΪ������NΪֵ��ĺ�����ϵ���ǣ� ��
A.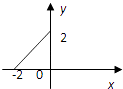
B.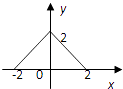
C.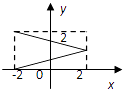
D.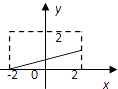
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ij��ַ��������ǵij��У��������о����ϲ����Ϊ����ijУ��ѧ���Թ���������ʹ��������Ӹ�У8000��ѧ���а��꼶�÷ֲ�����ķ�ʽ�����ȡ��100λͬѧ���е��飬�õ���100��ͬѧÿ��ʹ�ù���������ʱ�䣨��λ��Сʱ�������
ʹ��ʱ�� |
|
|
|
|
|
���� | 10 | 40 | 25 | 20 | 5 |
������֪��У��һѧ����2400�ˣ����ȡ��100��ѧ���д�һѧ��������
����������Щ���ݵ�Ƶ�ʷֲ�ֱ��ͼ��
�����Ƹ�У��ѧ��ÿ��ʹ�ù���������ƽ��ʱ��![]() ��ͬһ���е������ø���������е�ֵ����������
��ͬһ���е������ø���������е�ֵ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() Ϊ��������ͼ����
Ϊ��������ͼ����![]() �������߷���Ϊ
�������߷���Ϊ![]() .
.
��1���жϺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
��2����֪![]() ����
����![]() ����������
����������![]() ������
������![]() ��
�� ![]() ��
��![]() ��ǡ��һ�����������ʵ��
��ǡ��һ�����������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
��![]() Ϊʵ����
Ϊʵ����![]() ��
��![]() ��
��
��1��������![]() ��ͼ�����
��ͼ�����![]() ���ҷ���
���ҷ���![]() ����ֻ��һ��ʵ������
����ֻ��һ��ʵ������![]() �ı���ʽ��
�ı���ʽ��
��2���ڣ�1���������£���![]() ʱ��
ʱ��![]() �ǵ�����������ʵ��
�ǵ�����������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=max{x2��ax+a��ax��a+1}������max{x��y}= ![]() �� ������������x��R������f��x��=x2��ax+a����ʵ��a��ֵ��
�� ������������x��R������f��x��=x2��ax+a����ʵ��a��ֵ��
������a��1����f��x������Сֵm��a����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=a�� ![]() ��a��R��
��a��R��
��1���жϺ���f��x���ĵ����Բ�����֤����
��2��������f��x�����溯������f��x���� ![]() ��x��[1��2]ʱ���������m�����ֵ��
��x��[1��2]ʱ���������m�����ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com