
【题目】如图,在四棱锥![]() 中
中![]() ,且
,且![]() 和
和![]() 分别是棱
分别是棱![]() 和
和![]() 的中点.
的中点.
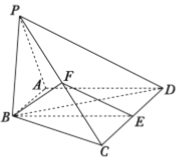
(Ⅰ)求证:![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
【答案】(Ⅰ)见证明;(Ⅱ)![]()
【解析】
(Ⅰ)先证明四边形![]() 为矩形,得到
为矩形,得到![]() ,然后又可证得
,然后又可证得![]() 平面
平面![]() ,再根据
,再根据![]() 得到
得到![]() 平面
平面![]() ,于是
,于是![]() ,进而得到
,进而得到![]() ,所以有
,所以有![]() 平面
平面![]() ,于是可得所证结论成立.(Ⅱ)建立空间直角坐标系,根据题中条件得到相关点的坐标,求出平面
,于是可得所证结论成立.(Ⅱ)建立空间直角坐标系,根据题中条件得到相关点的坐标,求出平面![]() 的法向量和直线
的法向量和直线![]() 的方向向量
的方向向量![]() ,根据两向量夹角的余弦值可求出线面角的正弦值.
,根据两向量夹角的余弦值可求出线面角的正弦值.
(Ⅰ)∵![]() 为
为![]() 中点,
中点,![]() ,
,
∴![]() .
.
又![]() ,
,
∴四边形![]() 为平行四边形.
为平行四边形.
∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∴四边形![]() 为矩形,
为矩形,
∴![]() .
.
由![]() 得
得![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() ,
,
∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() .
.
(Ⅱ)由(Ⅰ)知![]() 平面
平面![]() .
.
以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,平面
轴,平面![]() 内过点
内过点![]() 且与
且与![]() 的垂线为
的垂线为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,如图所示.
,如图所示.

∵![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() .
.
∴点![]() 到
到![]() 轴的距离为
轴的距离为![]() .
.
∴![]() 同时知
同时知![]() .
.
又![]() ,
,
∴![]() .
.
∴![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由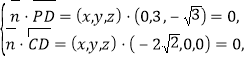 得
得![]()
令![]() 则
则![]() .
.
又![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
则 .
.
即直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取的5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5位女性中,再随机抽取3人赠送礼品,试求抽取3人中恰有2人位“微信控”的概率.
参考公式: 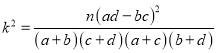 ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]()
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)①证明:当![]() 时,函数
时,函数![]() 在
在![]() 上恰有一个极值点
上恰有一个极值点![]() ;
;
②求实数![]() 的取值范围,使得对任意的
的取值范围,使得对任意的![]() ,恒有
,恒有![]() 成立.
成立.
注:![]() 为自然对数的底数.
为自然对数的底数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了进一步激发同学们的学习热情,某班级建立了数学英语两个学习兴趣小组,两组的人数如下表所示:
组别 性别 | 数学 | 英语 |
男 | 5 | 1 |
女 | 3 | 3 |
现采用分层抽样的方法(层内采用简单随机抽样)从两组中共抽取3名同学进行测试.
(1)求从数学组抽取的同学中至少有1名女同学的概率;
(2)记ξ为抽取的3名同学中男同学的人数,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,底面
,底面![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 中点,点
中点,点![]() 在线段
在线段![]() 上.
上.
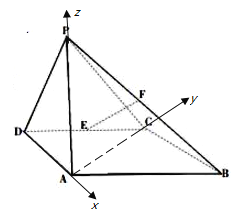
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]()
![]()
![]()
![]() ,求实数
,求实数![]() 使直线
使直线![]() 与平面
与平面![]() 所成角和直线
所成角和直线![]() 与平面
与平面![]() 所成角相等.
所成角相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,抛物线
,抛物线![]() :
: ![]() 与抛物线
与抛物线![]() :
: ![]() 异于原点
异于原点![]() 的交点为
的交点为![]() ,且抛物线
,且抛物线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)若直线![]() 与抛物线
与抛物线![]() 交于点
交于点![]() ,
, ![]() ,且
,且![]() ,求
,求![]() ;
;
(2)证明: ![]() 的面积与四边形
的面积与四边形![]() 的面积之比为定值.
的面积之比为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个说法,其中正确的说法是( )
A.残差点分布的带状区域的宽度越窄相关指数越小;
B.在刻画回归模型的拟合效果时,相关指数![]() 的值越大,说明拟合的效果越好;
的值越大,说明拟合的效果越好;
C.在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均增加0.2个单位;
平均增加0.2个单位;
D.对分类变量![]() 与
与![]() ,若它们的随机变量
,若它们的随机变量![]() 的观测值
的观测值![]() 越小,则判断“
越小,则判断“![]() 与
与![]() 有关系”的把握程度越大.
有关系”的把握程度越大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小张、小李、小华、小明四人玩轮流投掷一枚标准色子的游戏.若有一人投到的数最小,且无人与他并列,则判他获胜;若投出最小数的人多于一个,则将没投出最小数的人先淘汰,再让剩下的人重新做一轮游戏,这样不断地进行下去,直到某个人胜出为止.已知第一个投掷色子的小张投到了数3.则他获胜的概率是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com