
【题目】设函数![]() ,
,![]()
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)①证明:当![]() 时,函数
时,函数![]() 在
在![]() 上恰有一个极值点
上恰有一个极值点![]() ;
;
②求实数![]() 的取值范围,使得对任意的
的取值范围,使得对任意的![]() ,恒有
,恒有![]() 成立.
成立.
注:![]() 为自然对数的底数.
为自然对数的底数.
【答案】(1)![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,(2)①证明见解析;②
,(2)①证明见解析;②![]() .
.
【解析】
(1)求导后,由![]() 得递增区间,由
得递增区间,由![]() 得递减区间;
得递减区间;
(2)①求导两次后,利用零点存在性定理和极值点的概念可证结论;②当![]()
![]() 时,根据单调性可知不合题意,当
时,根据单调性可知不合题意,当![]() 时,利用①的结论,可知
时,利用①的结论,可知![]() 在
在![]() 上的最大值为
上的最大值为![]() ,再将恒成立转化为最大值即可解决.
,再将恒成立转化为最大值即可解决.
(1)当![]() 时,
时,![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,
,
所以![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)①证明:当![]() 时,
时,![]() ,
,
令![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,
,
当![]() 时,
时,![]() ,,当
,,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
因为![]() ,
,![]()
![]()
![]() ,
,
根据零点存在性定理可知,函数![]()
![]() 在
在![]() 上有唯一实根,设为
上有唯一实根,设为![]() ,则
,则![]() ,
,
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,所以
上递增,所以![]() 在
在![]() 处取得极小值,
处取得极小值,
所以当![]() 时,函数
时,函数![]() 在
在![]() 上恰有一个极值点
上恰有一个极值点![]() .
.
②当![]() 时,
时,![]() ,由①知
,由①知![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上为增函数,所以
上为增函数,所以![]() ,
,
所以![]() 在
在![]() 上递增,所以
上递增,所以![]() 恒成立, 不合题意,
恒成立, 不合题意,
当![]() 时,由①知,函数
时,由①知,函数![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
设函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ,则
,则![]() ,
,
若对任意的![]() ,恒有
,恒有![]() 成立.
成立.
则![]() ,因为
,因为![]() ,所以由
,所以由![]() 得
得![]() ,
,
得![]() ,得
,得![]() ,得
,得![]() ,
,
因为![]() ,所以
,所以![]() .
.


科目:高中数学 来源: 题型:
【题目】某城市随机抽取一年(![]() 天)内
天)内![]() 天的空气质量指数
天的空气质量指数![]() 的监测数据,结果统计如下:
的监测数据,结果统计如下:
|
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
天数 |
|
|
|
|
|
|
|
(1)若某企业每天由空气污染造成的经济损失![]() (单位:元)与空气质量指数
(单位:元)与空气质量指数![]() (记为
(记为![]() )的关
)的关
系式为:

试估计在本年内随机抽取一天,该天经济损失![]() 大于
大于![]() 元且不超过
元且不超过![]() 元的概率;
元的概率;
(2)若本次抽取的样本数据有![]() 天是在供暖季,其中有
天是在供暖季,其中有![]() 天为重度污染,完成下面
天为重度污染,完成下面![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 |
|
附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上有奇数条线段,甲乙两人做如下游戏:两人轮流(甲先乙后)给任一条尚未设定方向的线段设定一个方向,直至某次(甲)设定后,所有线段各有了一个方向为止.如果最后得到的所有向量之和的模长不小于原来每条线段长,则甲获胜,否则乙获胜.问:谁有必胜策略?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两支围棋队各5名队员按事先排好的顺序进行擂台赛,双方1号队员先赛,负者被淘汰;然后负方的2号队员再与对方的胜者比赛,负者又被淘汰.依次类推,直到有一方队员全部被淘汰,则宣布另一方获胜.假设每名队员的实力相当,则比赛结束时甲队未上场队员数![]() 的数学期望
的数学期望![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在股票市场上,投资者常根据股价![]() 每股的价格
每股的价格![]() 走势图来操作,股民老张在研究某只股票时,发现其在平面直角坐标系内的走势图有如下特点:每日股价
走势图来操作,股民老张在研究某只股票时,发现其在平面直角坐标系内的走势图有如下特点:每日股价![]() 元
元![]() 与时间
与时间![]() 天
天![]() 的关系在ABC段可近似地用函数
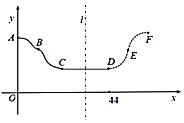
的关系在ABC段可近似地用函数![]() 的图象从最高点A到最低点C的一段来描述
的图象从最高点A到最低点C的一段来描述![]() 如图
如图![]() ,并且从C点到今天的D点在底部横盘整理,今天也出现了明显的底部结束信号.老张预测这只股票未来一段时间的走势图会如图中虚线DEF段所示,且DEF段与ABC段关于直线l:
,并且从C点到今天的D点在底部横盘整理,今天也出现了明显的底部结束信号.老张预测这只股票未来一段时间的走势图会如图中虚线DEF段所示,且DEF段与ABC段关于直线l:![]() 对称,点B,D的坐标分别是
对称,点B,D的坐标分别是![]() .
.
![]() 请你帮老张确定a,
请你帮老张确定a,![]() ,
,![]() 的值,并写出ABC段的函数解析式;
的值,并写出ABC段的函数解析式;
![]() 如果老张预测准确,且今天买入该只股票,那么买入多少天后股价至少是买入价的两倍?
如果老张预测准确,且今天买入该只股票,那么买入多少天后股价至少是买入价的两倍?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com