练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    试求直线l1：x-y-2=0关于直线l2：3x-y+3=0对称的直线l的方程．
    【答案】分析：先求得直线l2与直线l1对的交点A的坐标，然后用点斜式表示出l的方程，再由l1到l2与l到l2的角相等，求出斜率，即可求出方程．
    解答：解：解方程
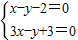
    解得
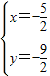
    ∴直线l2与直线l1对的交点为A（-，-）
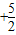
    设所求的直线l的方程为y+=k（x）即2kx-2y+5k-9=0，由题意知，l1到l2与l到l2的角相等，则
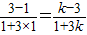
    ∴k=-7
    所以直线的方程为7x+y+22=0．
    点评：本题考查与直线关于点、直线对称的直线方程，用点斜式求直线的方程，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    试求直线l1：x-y-2=0关于直线l2：3x-y+3=0对称的直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源：学习高手必修二数学苏教版 苏教版 题型：044

    试求直线l1：x－y－2＝0关于直线3x－y＋3＝0对称的直线方程．

    查看答案和解析>>

    科目：高中数学 来源：天骄之路中学系列　读想用　高二数学(上) 题型：044

    试求直线l1：x－y－2＝0关于直线l2：3x－y＋3＝0对称的直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    试求直线l1：x-y-2=0关于直线l2：3x-y+3=0对称的直线l的方程．

    查看答案和解析>>

    同步练习册答案