分析:(1)利用图形关系直接可以计算;(2)解法一可以由(1)猜想结论,然后利用数学归纳法进行证明,解法二借助于表示出Bn、An的坐标,利用曲线xy=1,从而构建数列,探求其通项.
解答:解:(1)
OB1=2,B1B2=2(-1),B2B3=2(-).(4分)
(2)解法1:B
n-1B
n=a
n,猜想出
an=Bn-1Bn=2(-)当n=1时,由上已证猜想成立.
假设n=k时,猜想成立,即有
ak=2(-),(2分)
设S
k是a
n的前k项和,则有
(Sk+)•)•=1.
∴
(Sk-1+)•=1.
两式相减,得
+=-(3分)
即
+(-)=-(+).
∴
+4ak+1-4=0,
解得
ak+1=2(-),即n=k+1时,猜想也成立,(2分)
综合上述,所求的通项公式
an=Bn-1Bn=2(-).(1分)
解法2:设OB
1=a
1,B
1B
2=a
2,,B
n-1B
n=a
n,{a
n}的前n项和为S
n.侧B
n(S
n,0),∴
An+1(Sn+an+!,an+1).(3分)
代入曲线方程得:
(Sn+an+1)(an+1)=1,且(a1)2=1,(2分)
| | ∴2Snan+1+(an+1)2=4,a1=2, | | 2Sn(Sn+1-Sn)+(Sn+1-Sn)2=4,S1=2. |
| |
化简得(S
n+1)
2-(S
n)
2=4,(3分)
∴(S
n)
2=(S
1)
2+4(n-1)=4n,∴
Sn=2所求的通项公式为
an=Bn-1Bn=2(-).
点评:本题的解法一体现特殊到一般地思维,但结论的正确性必须有严密的证明;解法二的关键是构建数列,从而探求数列的通项.

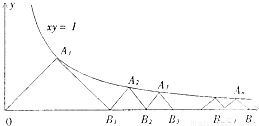
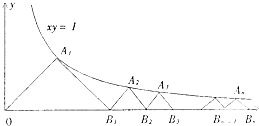 △A1OB1,△A2B1B2,△A3B2B3,…,△AnBn-1Bn均为等腰直角三角形,已知它们的直角顶点A1,A2,A3,…,An在曲线xy=1(x>0)上,B1,B2,B3,…,Bn在x轴上(如图),
△A1OB1,△A2B1B2,△A3B2B3,…,△AnBn-1Bn均为等腰直角三角形,已知它们的直角顶点A1,A2,A3,…,An在曲线xy=1(x>0)上,B1,B2,B3,…,Bn在x轴上(如图),

 口算能手系列答案
口算能手系列答案