
无穷数列 的首项是
的首项是 ,随后两项都是
,随后两项都是 ,接下来
,接下来 项都是
项都是 ,再接下来
,再接下来 项都是
项都是 , ,以此类推.记该数列为
, ,以此类推.记该数列为 ,若
,若 ,
, ,则
,则 .
.
科目:高中数学 来源: 题型:填空题
平面上有 条直线, 这
条直线, 这 条直线任意两条不平行, 任意三条不共点, 记这
条直线任意两条不平行, 任意三条不共点, 记这 条直线将平面分成
条直线将平面分成 部分, 则
部分, 则 ___________,
___________,  时,
时, _________________.)(用
_________________.)(用 表示).
表示).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知一个关于正整数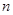 的命题
的命题 满足“若
满足“若 时命题
时命题 成立,则
成立,则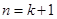 时命题
时命题 也成立”.有下列判断:
也成立”.有下列判断:
(1)当 时命题
时命题 不成立,则
不成立,则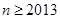 时命题
时命题 不成立;
不成立;
(2)当 时命题
时命题 不成立,则
不成立,则 时命题
时命题 不成立;
不成立;
(3)当 时命题
时命题 成立,则
成立,则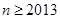 时命题
时命题 成立;
成立;
(4)当 时命题
时命题 成立,则
成立,则 时命题
时命题 成立.
成立.
其中正确判断的序号是 .(写出所有正确判断的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
在平面几何里,已知直角三角形ABC中,角C为
 ,AC=b,BC=a,运用类比方法探求空间中三棱锥的有关结论:
,AC=b,BC=a,运用类比方法探求空间中三棱锥的有关结论:
有三角形的勾股定理,给出空间中三棱锥的有关结论:________
若三角形ABC的外接圆的半径为 ,给出空间中三棱锥的有关结论:________
,给出空间中三棱锥的有关结论:________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com