Question

19．圆锥的底面半径为2cm，高为4cm，求圆锥的内接圆柱的侧面积的最大值．

Answer 1

分析 设内接圆柱的底面半径为r，高为h，根据三角形相似找出h与r的关系，然后表示出内接圆柱侧面积，最后利用基本不等式求出最值即可，注意等号成立的条件．

解答 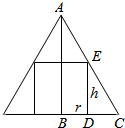解：设内接圆柱的底面半径为r，高为h，如右图，
∵△CAB∽△CED，
∴$\frac{ED}{AB}$=$\frac{CD}{CB}$，即$\frac{h}{4}$=$\frac{2-r}{2}$，则h=4-2r，
∴内接圆柱侧面积S=2πrh=2πr×（4-2r）=4πr（2-r）≤4π（$\frac{r+2-r}{2}$）²=4π，
当且仅当r=2-r，即r=1时取等号，
∴内接圆柱侧面积最大值是4π．

点评 本题主要考查了圆锥的内接圆柱的侧面积，以及基本不等式在最值中的应用，同时考查了分析问题的能力，属于中档题．