
【题目】已知函数![]()
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 有两个极值点
有两个极值点![]() ,证明:
,证明:![]()
【答案】(1)见解析;(2)证明见解析.
【解析】
(1)首先对函数求导,根据韦达定理与判别式确定二次函数根的分布,然后根据函数值的正负确定函数的单调性;
(2)首先求出![]() ,然后在对求出的表达式进行切线缩放即可证明不等式.
,然后在对求出的表达式进行切线缩放即可证明不等式.
(1)由题知函数的定义域为![]() ,
,
有![]() ,
,
对![]() 有
有![]() ,
,
当![]() 时
时![]() ,有
,有![]() ,
,
所以函数![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时
时![]() ,
,![]() 有两个根
有两个根![]() ,
,![]() ,设
,设![]() ,
,
根据韦达定理有![]() ,
,![]() ,
,
当![]() 时,
时,
![]() 有两个正根
有两个正根![]() ,
,![]() ,
,
可知当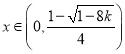 时
时![]() ,函数
,函数![]() 单调递增,
单调递增,
当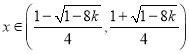 时
时![]() ,函数
,函数![]() 单调递减,
单调递减,
当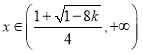 时
时![]() ,函数
,函数![]() 单调递增,
单调递增,
当![]() 时,
时,
![]() 有两个根
有两个根![]() ,
,![]() ,
,
可知当 时
时![]() ,函数
,函数![]() 单调递减,
单调递减,
可知当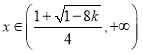 时
时![]() ,函数
,函数![]() 单调递增;
单调递增;
(2)由(1)知当![]() 时,函数有两个极值点
时,函数有两个极值点![]() ,
,![]() ,设
,设![]() ,
,
根据(1)中单调性可知函数![]() 在
在![]() 处取极大值,
处取极大值,![]() 处取极小值,
处取极小值,
所以![]() ,
,
代入![]() ,
,![]() ,
,
整理得![]() ,
,
令![]() ,有
,有![]() ,
,
有![]() ,
,
因为![]() ,
,
代入![]() 有
有![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)记函数![]() 的导函数是
的导函数是![]() ,若不等式
,若不等式![]() 对任意的实数
对任意的实数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,
,![]() 是函数
是函数![]() 的导函数,若函数
的导函数,若函数![]() 存在两个极值点
存在两个极值点![]() ,
,![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 上任意一点
上任意一点![]() 满足
满足![]() ,直线
,直线![]() 的方程为
的方程为![]() ,且与曲线
,且与曲线![]() 交于不同两点
交于不同两点![]() ,
,![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设点![]() ,直线
,直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且
,且![]() ,判断直线
,判断直线![]() 是否过定点?若过定点,求该定点的坐标.
是否过定点?若过定点,求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,该几何体是由一个直三棱柱ABE﹣DCF和一个四棱锥P﹣ABCD组合而成,其中EF=EA=EB=2,AE⊥EB,PA=PD![]() ,平面PAD∥平面EBCF.
,平面PAD∥平面EBCF.
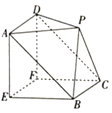
(1)证明:平面PBC∥平面AEFD;
(2)求直线AP与平面PCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1772年德国的天文学家波得发现了求太阳的行星距离的法则,记地球距离太阳的平均距离为10,可以算得当时已知的六大行星距离太阳的平均距离如下表:
星名 | 水星 | 金星 | 地球 | 火星 | 木星 | 土星 |
与太阳的距离 | 4 | 7 | 10 | 16 | 52 | 100 |
除水星外,其余各星与太阳的距离都满足波得定则(某一数列规律),当时德国数学家高斯根据此定则推算,火星和木星之间距离太阳28还有一颗大行星,1801年,意大利天文学家皮亚齐经过观测,果然找到了火星和木星之间距离太阳28的谷神星以及它所在的小行星带,请你根据这个定则,估算从水星开始由近到远算,第10个行星与太阳的平均距离大约是( )
A.388B.772C.1540D.3076
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了一款应用软件,为激发大家的学习兴趣,他们推出了“解数学题获取软件激活码”的活动,这款软件的激活码为下列数学问题的答案:已知数列1、1、2、1、2、4、8、1、2、4、8、16、……,其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,再接下来的三项是
,再接下来的三项是![]() ,……,以此类推,求满足如下条件的最小整数
,……,以此类推,求满足如下条件的最小整数![]() 且该数列的前
且该数列的前![]() 项和为2的整数幂,那么该软件的激活码是________。
项和为2的整数幂,那么该软件的激活码是________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,
为坐标原点,![]() 是抛物线
是抛物线![]() :
:![]() 的焦点,
的焦点,![]() 是抛物线
是抛物线![]() 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过![]() ,
,![]() ,
,![]() 三点的圆的圆心为
三点的圆的圆心为![]() .
.
(1)是否存在过点![]() ,斜率为
,斜率为![]() 的直线
的直线![]() ,使得抛物线
,使得抛物线![]() 上存在两点关于直线
上存在两点关于直线![]() 对称?若存在,求出
对称?若存在,求出![]() 的范围;若不存在,说明理由;
的范围;若不存在,说明理由;
(2)是否存在点![]() ,使得直线
,使得直线![]() 与抛物线
与抛物线![]() 相切于点
相切于点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com